题目内容
11.已知复数z满足(1-i)z=i2015(其中i为虚数单位),则$\overline{z}$的虚部为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}$i |
分析 利用复数的运算法则、共轭复数、虚部的定义即可得出.
解答 解:∵i4=1,∴i2015=(i4)503•i3=-i,
∴(1-i)z=i2015=-i,
∴$z=\frac{-i}{1-i}$=$\frac{-i(1+i)}{(1-i)(1+i)}$=$\frac{1-i}{2}$,
∴$\overline{z}$=$\frac{1}{2}+\frac{1}{2}i$,
则$\overline{z}$的虚部为$\frac{1}{2}$.
故选:A.
点评 本题考查了复数的运算法则、共轭复数、虚部的定义,属于基础题.

练习册系列答案
相关题目
6.若双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线y2=4bx的焦点分成5:3两段,则此双曲线的离心率为( )
| A. | $\frac{4\sqrt{15}}{15}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{15}$ | D. | $\sqrt{3}$ |
1.在实数0,-$\sqrt{3}$,-$\frac{2}{3}$,|-2|中,最小的数是( )
| A. | -$\frac{2}{3}$ | B. | 0 | C. | -$\sqrt{3}$ | D. | |-2| |
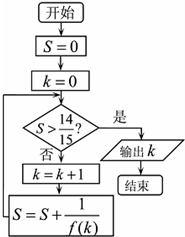 已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线与直线x+3y+2=0垂直.执行如图所示的程序框图,输出的k值是15.
已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线与直线x+3y+2=0垂直.执行如图所示的程序框图,输出的k值是15.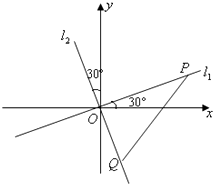 如图,过原点O的直线l1,l2分别与x轴,y轴成30°的角,点P(m,n)在l1上运动,点Q(p,q)在l2上运动,且$|PQ|=2\sqrt{2}$.
如图,过原点O的直线l1,l2分别与x轴,y轴成30°的角,点P(m,n)在l1上运动,点Q(p,q)在l2上运动,且$|PQ|=2\sqrt{2}$.