题目内容
【题目】已知函数f(x)=|x﹣a|,g(x)=ax,(a∈R).
(1)若函数y=f(x)是偶函数,求出符合条件的实数a的值;
(2)若方程f(x)=g(x)有两解,求出实数a的取值范围;
(3)若a>0,记F(x)=g(x)f(x),试求函数y=F(x)在区间[1,2]上的最大值.
【答案】
(1)解:∵函数f(x)=|x﹣a|为偶函数,
∴对任意的实数x,f(﹣x)=f(x)成立
即|﹣x﹣a|=|x﹣a|,
∴x+a=x﹣a恒成立,或x+a=a﹣x恒成立
∵x+a=a﹣x不能恒成立
∴x+a=x﹣a恒成立,得a=0
(2)解:当a>0时,|x﹣a|﹣ax=0有两解,
等价于方程(x﹣a)2﹣a2x2=0在(0,+∞)上有两解,
即(a2﹣1)x2+2ax﹣a2=0在(0,+∞)上有两解,
令h(x)=(a2﹣1)x2+2ax﹣a2,
因为h(0)=﹣a2<0,所以 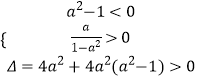 ,故0<a<1;
,故0<a<1;
同理,当a<0时,得到﹣1<a<0;
当a=0时,f(x)=|x|=0=g(x),显然不合题意,舍去.
综上可知实数a的取值范围是(﹣1,0)∪(0,1).
(3)解:令F(x)=f(x)g(x)
①当0<a≤1时,则F(x)=a(x2﹣ax),
对称轴 ![]() ,函数在[1,2]上是增函数,
,函数在[1,2]上是增函数,
所以此时函数y=F(x)的最大值为4a﹣2a2.
②当1<a≤2时, ![]() ,对称轴
,对称轴 ![]() ,
,
所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,F(1)=a2﹣a,F(2)=4a﹣2a2,
1)若F(1)<F(2),即 ![]() ,此时函数y=F(x)的最大值为4a﹣2a2;
,此时函数y=F(x)的最大值为4a﹣2a2;
2)若F(1)≥F(2),即 ![]() ,此时函数y=F(x)的最大值为a2﹣a.
,此时函数y=F(x)的最大值为a2﹣a.
③当2<a≤4时,F(x)=﹣a(x2﹣ax)对称轴 ![]() ,
,
此时 ![]() ,
,
④当a>4时,对称轴 ![]() ,此时
,此时 ![]() .
.
综上可知,函数y=F(x)在区间[1,2]上的最大值 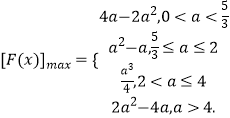
【解析】(1)根据函数为偶函数,f(﹣x)=f(x)对任意实数x恒成立,即|﹣x﹣a|=|x﹣a|任意实数x成立,去绝对值然后比较系数,可得a=0;(2)分三种情况加以讨论:当a>0时,将方程f(x)=g(x)两边平方,得方程(x﹣a)2﹣a2x2=0在(0,+∞)上有两解,构造新函数h(x)=(a2﹣1)x2+2ax﹣a2 , 通过讨论h(x)图象的对称轴方程和顶点坐标,可得0<a<﹣1;当a<0时,用同样的方法得到﹣1<a<0;而当a=0时代入函数表达式,显然不合题意,舍去.最后综合实数a的取值范围;(3)F(x)=f(x)g(x)=ax|x﹣a|,根据实数a与区间[1,2]的位置关系,分4种情况加以讨论:①当0<a≤1时,则F(x)=a(x2﹣ax),根据函数的单调增的性质,可得y=F(x)的最大值为F(2)=4a﹣2a2; ②当1<a≤2时,化成两个二次表达式的分段函数表达式,其对称轴为 ![]() ,得到所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,最大值决定于F(1)与F(2)大小关系.因此再讨论:当
,得到所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,最大值决定于F(1)与F(2)大小关系.因此再讨论:当 ![]() 时,y=F(x)的最大值为F(2)=4a﹣2a2;当
时,y=F(x)的最大值为F(2)=4a﹣2a2;当 ![]() 时,y=F(x)的最大值为F(1)=a2﹣a;③当2<a≤4时,F(x)=﹣a(x2﹣ax),图象开口向下,对称轴
时,y=F(x)的最大值为F(1)=a2﹣a;③当2<a≤4时,F(x)=﹣a(x2﹣ax),图象开口向下,对称轴 ![]() ,恰好在对称轴处取得最大值:
,恰好在对称轴处取得最大值: ![]() ;④当a>4时,F(x)=﹣a(x2﹣ax),图象开口向下,对称轴
;④当a>4时,F(x)=﹣a(x2﹣ax),图象开口向下,对称轴 ![]() ,在区间[1,2]上函数是增函数,故最大值为F(2)=2a2﹣4a.最后综止所述,可得函数y=F(x)在区间[1,2]上的最大值的结论.
,在区间[1,2]上函数是增函数,故最大值为F(2)=2a2﹣4a.最后综止所述,可得函数y=F(x)在区间[1,2]上的最大值的结论.
【考点精析】本题主要考查了奇偶性与单调性的综合和二次函数的性质的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案