题目内容
.设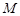 是椭圆
是椭圆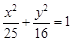 上的一点,
上的一点,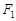 、
、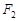 为焦点,
为焦点,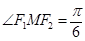 ,则
,则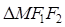
的面积为 ( )
( )
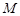 是椭圆
是椭圆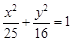 上的一点,
上的一点,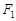 、
、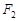 为焦点,
为焦点,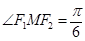 ,则
,则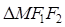
的面积为
 ( )
( )A.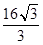 | B.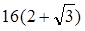 | C.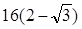 | D.16 |
C
解:因为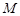 是椭圆
是椭圆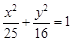 上的一点,
上的一点, 、
、 为焦点,
为焦点,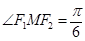 ,则利用椭圆的定义和余弦定理可知
,则利用椭圆的定义和余弦定理可知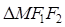 的面积为S=b2
的面积为S=b2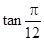 =
=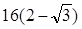 ,选C
,选C
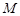 是椭圆
是椭圆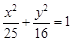 上的一点,
上的一点,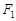 、
、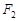 为焦点,
为焦点,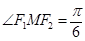 ,则利用椭圆的定义和余弦定理可知
,则利用椭圆的定义和余弦定理可知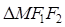 的面积为S=b2
的面积为S=b2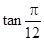 =
=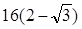 ,选C
,选C
练习册系列答案
相关题目
题目内容
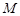 是椭圆
是椭圆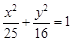 上的一点,
上的一点,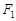 、
、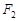 为焦点,
为焦点,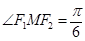 ,则
,则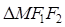
 ( )
( )A.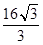 | B.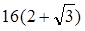 | C.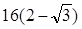 | D.16 |
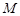 是椭圆
是椭圆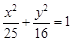 上的一点,
上的一点, 、
、 为焦点,
为焦点,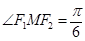 ,则利用椭圆的定义和余弦定理可知
,则利用椭圆的定义和余弦定理可知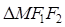 的面积为S=b2
的面积为S=b2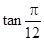 =
=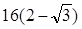 ,选C
,选C