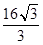题目内容
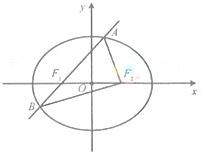
以椭圆的右焦点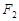 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
若过椭圆左焦点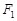 的直线MF1是圆
的直线MF1是圆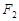 的切线,则椭圆的离心率为
的切线,则椭圆的离心率为
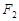 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,若过椭圆左焦点
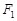 的直线MF1是圆
的直线MF1是圆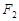 的切线,则椭圆的离心率为
的切线,则椭圆的离心率为 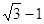
本题主要考查了直线与圆锥曲线的综合问题.考查学生分析问题、解决问题的能力
由题意根据椭圆的定义和焦半径和圆的半径关系得:|MF2|=|OF2|=c,|MF1|+|MF2|=2a,|F1F2|=2c,然后利用过椭圆左焦点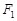 的直线MF1是圆
的直线MF1是圆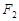 的切线,则利用垂直关系得到直角三角形MF1F2结合勾股定理得到,|MF1|2+|MF2|2=|F1F2|2,即(2a-c)2+c2=4c2,整理得2a2-2ac-c2=0,即e2+2e-2=0,解得e=
的切线,则利用垂直关系得到直角三角形MF1F2结合勾股定理得到,|MF1|2+|MF2|2=|F1F2|2,即(2a-c)2+c2=4c2,整理得2a2-2ac-c2=0,即e2+2e-2=0,解得e=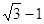 。故答案为
。故答案为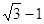 。
。
解决该试题的关键是先根据题意和椭圆定义可知|MF2|=|OF2|=c,|MF1|+|MF2|=2a,|F1F2|="2c" 进而根据勾股定理建立等式求得e。
由题意根据椭圆的定义和焦半径和圆的半径关系得:|MF2|=|OF2|=c,|MF1|+|MF2|=2a,|F1F2|=2c,然后利用过椭圆左焦点
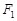 的直线MF1是圆
的直线MF1是圆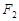 的切线,则利用垂直关系得到直角三角形MF1F2结合勾股定理得到,|MF1|2+|MF2|2=|F1F2|2,即(2a-c)2+c2=4c2,整理得2a2-2ac-c2=0,即e2+2e-2=0,解得e=
的切线,则利用垂直关系得到直角三角形MF1F2结合勾股定理得到,|MF1|2+|MF2|2=|F1F2|2,即(2a-c)2+c2=4c2,整理得2a2-2ac-c2=0,即e2+2e-2=0,解得e=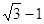 。故答案为
。故答案为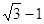 。
。解决该试题的关键是先根据题意和椭圆定义可知|MF2|=|OF2|=c,|MF1|+|MF2|=2a,|F1F2|="2c" 进而根据勾股定理建立等式求得e。

练习册系列答案
相关题目
 :
: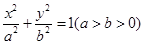 的左焦点为
的左焦点为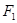 ,右焦点为
,右焦点为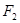 ,离心率
,离心率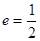 .过
.过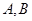 两点,且△
两点,且△ 的周长为
的周长为 .
.
 :
: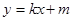 与椭圆
与椭圆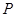 ,且与直线
,且与直线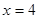 相交于点
相交于点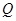 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点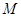 ,使得以
,使得以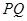 为直径的圆恒过点
为直径的圆恒过点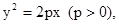 过焦点
过焦点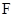 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值; 两点, 存在定点
两点, 存在定点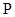 , 使得
, 使得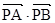 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.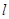 与椭圆
与椭圆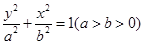 交于
交于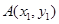 ,
,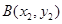 两点,已知
两点,已知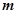
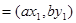 ,
,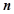
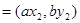 ,若
,若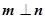 且椭圆的离心率
且椭圆的离心率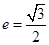 ,又椭圆经过点
,又椭圆经过点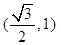 ,
,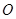 为坐标原点.
为坐标原点.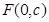 (
(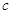 为半焦距),求直线
为半焦距),求直线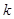 的值;
的值;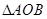 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由. 的离心率为
的离心率为 ,且过点(
,且过点( ),
), 与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.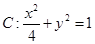 ,左右焦点分别为
,左右焦点分别为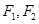 ,
,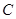 上一点
上一点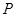 满足
满足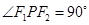 ,求
,求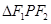 的面积;
的面积;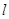 交
交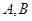 ,线段
,线段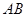 的中点为
的中点为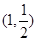 ,求直线
,求直线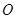 ,点
,点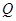 是圆内异于
是圆内异于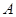 是圆周上一点.把纸片折叠使点
是圆周上一点.把纸片折叠使点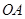 交于
交于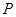 点.当点
点.当点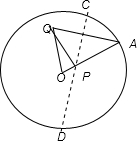
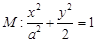
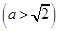 的右焦点为
的右焦点为 ,直线
,直线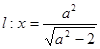 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点). 的方程;
的方程;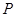 是椭圆
是椭圆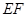 为圆
为圆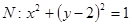 的任意一条直径(
的任意一条直径(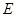 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.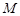 是椭圆
是椭圆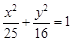 上的一点,
上的一点,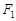 、
、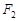 为焦点,
为焦点,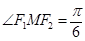 ,则
,则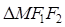
 ( )
( )