题目内容
过椭圆 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________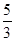
解:椭圆 的右焦点(1,0),直线AB的方程为y-0=2(x-1),
的右焦点(1,0),直线AB的方程为y-0=2(x-1),
即 y=2x-2,代入椭圆 化简可得6x2-10x=0,
化简可得6x2-10x=0,
∴x1+x2=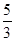 ,x1•x2=0,∴AB=" 1+4" • (x1+x2)2-4 x1•x2 =
,x1•x2=0,∴AB=" 1+4" • (x1+x2)2-4 x1•x2 =  ,
,
O到直线AB的距离d=|0-0-2| =
= ,故△OAB的面积为
,故△OAB的面积为  •AB•d==
•AB•d==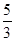 .
.
 的右焦点(1,0),直线AB的方程为y-0=2(x-1),
的右焦点(1,0),直线AB的方程为y-0=2(x-1),即 y=2x-2,代入椭圆
 化简可得6x2-10x=0,
化简可得6x2-10x=0,∴x1+x2=
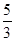 ,x1•x2=0,∴AB=" 1+4" • (x1+x2)2-4 x1•x2 =
,x1•x2=0,∴AB=" 1+4" • (x1+x2)2-4 x1•x2 =  ,
,O到直线AB的距离d=|0-0-2|
 =
= ,故△OAB的面积为
,故△OAB的面积为  •AB•d==
•AB•d==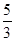 .
.
练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
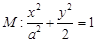
 的右焦点为
的右焦点为 ,直线
,直线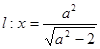 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点). 的方程;
的方程;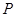 是椭圆
是椭圆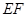 为圆
为圆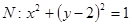 的任意一条直径(
的任意一条直径(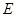 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值. 在
在 轴的非负半轴上,点
轴的非负半轴上,点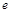 ;
; 为焦点
为焦点 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使 是椭圆
是椭圆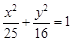 上的一点,
上的一点, 、
、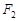 为焦点,
为焦点,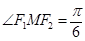 ,则
,则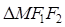
 ( )
( )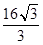
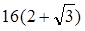
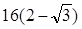
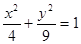 于A、B两点,且M为AB的中点,则直线l方程为 .
于A、B两点,且M为AB的中点,则直线l方程为 .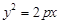 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( ) ,
, ,曲线
,曲线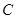 上的动点
上的动点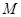 满足
满足 ,直线
,直线 与曲线
与曲线 .
. ,若
,若
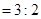 ,求直线
,求直线 的方程.
的方程. (
(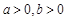 )的一条渐近线方程为
)的一条渐近线方程为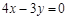 ,则该双曲
,则该双曲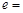 _________.
_________.