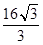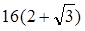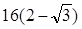题目内容
已知直线 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点,
若 的最小值为2,则其离心率为( )
的最小值为2,则其离心率为( )
 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点,若
 的最小值为2,则其离心率为( )
的最小值为2,则其离心率为( )A. | B. | C.2 | D.3 |
B
因为直线 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点,
若 的最小值为2,则||AB|最小时为通径长
的最小值为2,则||AB|最小时为通径长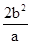 ,因此其离心率为
,因此其离心率为 ,选B
,选B
 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点,若
 的最小值为2,则||AB|最小时为通径长
的最小值为2,则||AB|最小时为通径长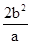 ,因此其离心率为
,因此其离心率为 ,选B
,选B
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与椭圆
与椭圆 交于
交于 ,
,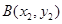 两点,已知
两点,已知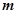
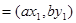 ,
,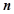
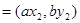 ,若
,若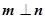 且椭圆的离心率
且椭圆的离心率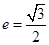 ,又椭圆经过点
,又椭圆经过点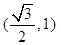 ,
,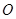 为坐标原点.
为坐标原点.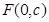 (
(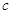 为半焦距),求直线
为半焦距),求直线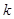 的值;
的值;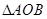 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.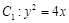 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆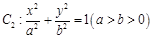 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为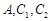 在第一象限的交点为
在第一象限的交点为 为坐标原点,且
为坐标原点,且 的面积为
的面积为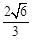
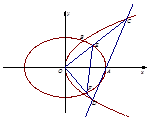
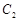 的标准方程;
的标准方程;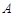 作直线
作直线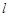 交
交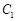 于
于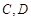 两点,射线
两点,射线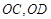 分别交
分别交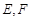 两点.
两点. 点在以
点在以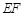 为直径的圆的内部;
为直径的圆的内部;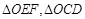 的面积分别为
的面积分别为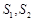 ,问是否存在直线
,问是否存在直线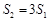 ?请说明理由.
?请说明理由.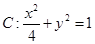 ,左右焦点分别为
,左右焦点分别为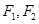 ,
,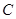 上一点
上一点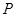 满足
满足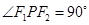 ,求
,求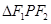 的面积;
的面积;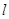 交
交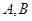 ,线段
,线段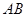 的中点为
的中点为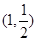 ,求直线
,求直线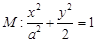
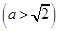 的右焦点为
的右焦点为 ,直线
,直线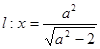 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点). 的方程;
的方程; 是椭圆
是椭圆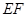 为圆
为圆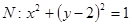 的任意一条直径(
的任意一条直径(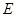 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.
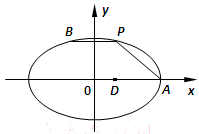
 中,已知点
中,已知点 为椭圆
为椭圆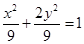 的右顶点, 点
的右顶点, 点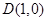 ,点
,点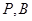 在椭
在椭 .
.
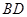 的方程;
的方程;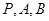 三点的圆
三点的圆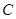 截得的弦长;
截得的弦长;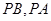 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由. 在
在 轴的非负半轴上,点
轴的非负半轴上,点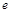 ;
; 为焦点
为焦点 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使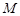 是椭圆
是椭圆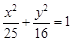 上的一点,
上的一点,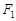 、
、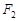 为焦点,
为焦点,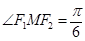 ,则
,则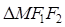
 ( )
( )