题目内容
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,
,![]() ,则称
,则称![]() 为“D-数列”.
为“D-数列”.
(1) 举出一个前五项均不为零的“D-数列”(只要求依次写出该数列的前五项);
(2) 若“D-数列”![]() 中,
中,![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,写出数列
,写出数列![]() 的通项公式,并分别判断当
的通项公式,并分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在,如果存在,求出其极限值(若不存在不需要交代理由);
的极限是否存在,如果存在,求出其极限值(若不存在不需要交代理由);
(3) 证明: 设“D-数列”![]() 中的最大项为
中的最大项为![]() ,证明:
,证明: ![]() 或
或![]() .
.
【答案】(1) ![]() ;(2)
;(2) 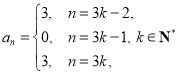 ,
,![]() 不存在,
不存在,![]() 存在,
存在,![]() ;(3) 证明见解析.
;(3) 证明见解析.
【解析】
(1)依照定义写出数列即可.
(2)计算可得![]() 为周期数列,且周期为3,故可得
为周期数列,且周期为3,故可得![]() 与
与![]() 的通项公式,根据通项公式可判断数列的极限存在与否.
的通项公式,根据通项公式可判断数列的极限存在与否.
(3)利用反证法可证明![]() 或
或![]() .
.
(1) 如![]() 等等.
等等.
(2) 因为![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,
故![]() 为周期数列,且周期为3,其通项公式为
为周期数列,且周期为3,其通项公式为![]() .
.
![]() 的极限不存在.
的极限不存在.
而![]() 时,
时,![]() ,所以
,所以![]() 的极限存在,
的极限存在,![]() .
.
(3) 由题设有![]() 或
或![]() .
.
假设![]() 且
且![]() .
.
注意到![]() .
.
故对一切![]() ,均有
,均有![]() ,这与
,这与![]() 的最大项为
的最大项为![]() 矛盾,从而假设不成立,
矛盾,从而假设不成立,![]() 或
或![]() .
.

练习册系列答案
相关题目