题目内容
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,直线
的焦点,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ,连接
,连接![]() 交抛物线于另一点
交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 的垂线交抛物线
的垂线交抛物线![]() 于另一点
于另一点![]() .
.
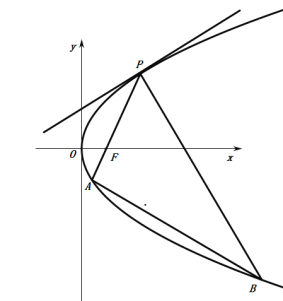
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)求三角形![]() 面积
面积![]() 的最小值.
的最小值.
【答案】(1)![]() ,(2)16
,(2)16
【解析】
(1)求得![]() ,再设直线
,再设直线![]() 的方程,联立抛物线方程令二次方程
的方程,联立抛物线方程令二次方程![]() 求解即可.
求解即可.
(2)设切线![]() 的方程为
的方程为![]() ,
,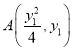 ,
,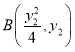 ,根据
,根据![]() ,
,![]() ,
,![]() 三点共线求得
三点共线求得![]() ,再化简求得
,再化简求得![]() 到直线
到直线![]() 的距离,进而表达出三角形
的距离,进而表达出三角形![]() 面积,再利用基本不等式的方法求最小值即可.
面积,再利用基本不等式的方法求最小值即可.
(1)由![]() 得
得![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
由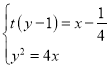 得
得![]() ,
,
因为直线![]() 与抛物线
与抛物线![]() 相切,故
相切,故![]() ,解得
,解得![]() .
.
故所求直线![]() 的方程
的方程![]() ,即
,即![]() .
.
(2)设切线![]() 的方程为
的方程为![]() ,
,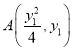 ,
,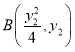 ,
,
又由![]() ,
,![]() ,
,![]() 三点共线,故
三点共线,故![]() ,
,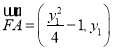 ,
, ,
,
化简可得,![]() ,
,
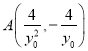 ,
,
由 得
得![]() ,
,
因为直线![]() 与抛物线
与抛物线![]() 相切,故
相切,故![]() ,即
,即![]() ,
,
故直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
因此点![]() 到直线
到直线![]() 的距离为
的距离为
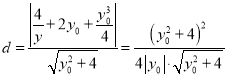 ,
,
由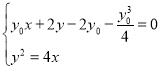 得
得![]() ,
,![]() ,
,![]() ,
,
故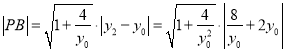 ,
,
所以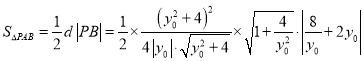
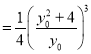
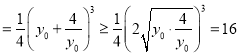 等号成立当且仅当
等号成立当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
此时三角形![]() 面积
面积![]() 的最小值为16.
的最小值为16.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目