题目内容
已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
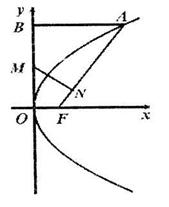
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标。

(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标。
(1)抛物线方程为y2=4x
(2)N的坐标(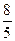 ,
, )
)
(2)N的坐标(
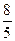 ,
, )
)(1)抛物线y2=2px的准线为x= - ,于是4+
,于是4+ =5,∴p=2.
=5,∴p=2.
∴抛物线方程为y2=4x……6分
(2)∵点A是坐标是(4,4),由题意得B(0,4),M(0,2),
又∵F(1,0),∴kFA= ;MN⊥FA,∴kMN=-
;MN⊥FA,∴kMN=- ,
,
则FA的方程为y= (x-1),MN的方程为y-2= -
(x-1),MN的方程为y-2= - x,
x,
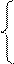
 y=
y= (x-1) x=
(x-1) x=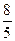
解方程组 ,得
y-2= - x y=
x y=
∴N的坐标(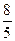 ,
, )…….12分
)…….12分
 ,于是4+
,于是4+ =5,∴p=2.
=5,∴p=2.∴抛物线方程为y2=4x……6分
(2)∵点A是坐标是(4,4),由题意得B(0,4),M(0,2),
又∵F(1,0),∴kFA=
 ;MN⊥FA,∴kMN=-
;MN⊥FA,∴kMN=- ,
,则FA的方程为y=
 (x-1),MN的方程为y-2= -
(x-1),MN的方程为y-2= - x,
x,
 y=
y= (x-1) x=
(x-1) x=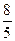
解方程组 ,得
y-2= -
 x y=
x y=
∴N的坐标(
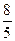 ,
, )…….12分
)…….12分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
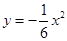 的准线方程为 。
的准线方程为 。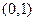 与抛物线
与抛物线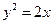 有且只有一个公共点的直线的条数是( )
有且只有一个公共点的直线的条数是( )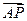 =l
=l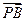 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1),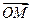 =
=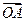 +
+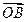 ,O为坐标原点.
,O为坐标原点.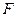 是抛物线
是抛物线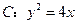 的焦点,过
的焦点,过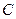 于
于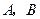 两点。设
两点。设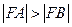 ,则
,则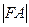 与
与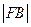 的比值等于 。
的比值等于 。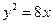 的焦点为
的焦点为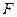 ,准线为
,准线为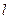 ,
,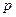 为抛物线上一点,
为抛物线上一点,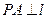 ,
,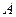 为垂足,如果直线
为垂足,如果直线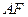 斜率为
斜率为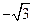 ,那么
,那么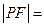
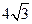
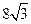
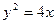 上一点
上一点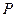 引其准线的垂线,垂足为
引其准线的垂线,垂足为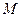 ,设抛物线的焦点为
,设抛物线的焦点为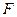 ,且
,且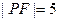 ,则
,则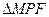 的面积为
的面积为
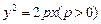 的焦点为
的焦点为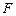 ,准线
,准线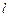 与
与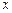 轴交于点
轴交于点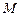 ,若
,若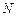 为
为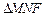 为等腰三角形,
为等腰三角形,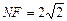 时,则
时,则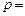 _____.
_____.