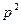题目内容
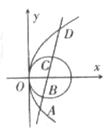
已知抛物线y=x2上的两点A、B满足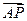 =l
=l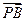 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1),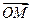 =
=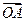 +
+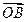 ,O为坐标原点.
,O为坐标原点.
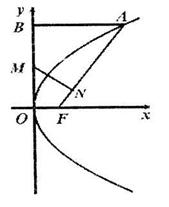
(I) 求四边形OAMB的面积的最小值;
(II) 求点M的轨迹方程.
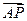 =l
=l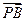 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1),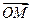 =
=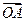 +
+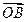 ,O为坐标原点.
,O为坐标原点.(I) 求四边形OAMB的面积的最小值;
(II) 求点M的轨迹方程.
(1)2(2)y=x2+2
(Ⅰ)由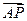 =l
=l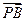 知A、P、B三点在同一条直线上,设该直线方程为y=kx+1,A(x1,x12),B(x2,x22).
知A、P、B三点在同一条直线上,设该直线方程为y=kx+1,A(x1,x12),B(x2,x22).
由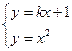 得x2-kx-1=0,\x1+x2=k,x1x2=-1,\
得x2-kx-1=0,\x1+x2=k,x1x2=-1,\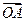 ·
·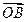 =x1x2+x12x22=-1+(-1)2=0,\
=x1x2+x12x22=-1+(-1)2=0,\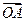 ^
^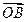 .
.
又OAMB是平行四边形,\四边形OAMB是矩形,
\S=|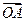 |·|
|·|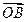 |=
|=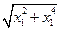 ·
·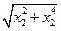 =-x1x2
=-x1x2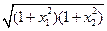
=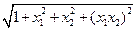 =
=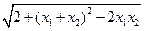 =
=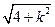 .
.
\当k=0时,S取得最小值是2. 6分
(Ⅱ)设M(x,y),\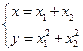 ,消去x1和x2得x2=y-2,\点M的轨迹是y=x2+2 6分
,消去x1和x2得x2=y-2,\点M的轨迹是y=x2+2 6分
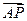 =l
=l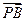 知A、P、B三点在同一条直线上,设该直线方程为y=kx+1,A(x1,x12),B(x2,x22).
知A、P、B三点在同一条直线上,设该直线方程为y=kx+1,A(x1,x12),B(x2,x22).由
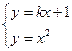 得x2-kx-1=0,\x1+x2=k,x1x2=-1,\
得x2-kx-1=0,\x1+x2=k,x1x2=-1,\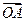 ·
·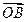 =x1x2+x12x22=-1+(-1)2=0,\
=x1x2+x12x22=-1+(-1)2=0,\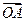 ^
^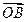 .
.又OAMB是平行四边形,\四边形OAMB是矩形,
\S=|
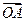 |·|
|·|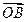 |=
|=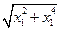 ·
·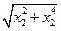 =-x1x2
=-x1x2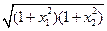
=
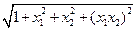 =
=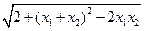 =
=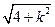 .
.\当k=0时,S取得最小值是2. 6分
(Ⅱ)设M(x,y),\
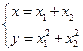 ,消去x1和x2得x2=y-2,\点M的轨迹是y=x2+2 6分
,消去x1和x2得x2=y-2,\点M的轨迹是y=x2+2 6分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
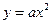 的焦点坐标为
的焦点坐标为 ,则实数
,则实数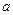 的值为 .
的值为 .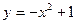
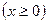 上找一点P
上找一点P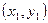 ,其中
,其中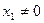 ,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )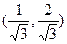
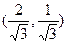
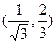
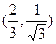
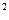 =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )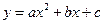 通过点
通过点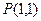 ,且在点
,且在点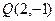 处与直线
处与直线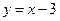 相切,求实数a、b、c的值.
相切,求实数a、b、c的值.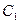 :
: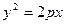 和圆
和圆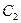 :
: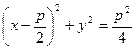 ,其中
,其中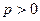 ,直线
,直线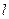 经过
经过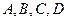 四点,则
四点,则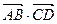 的值为 ( )
的值为 ( )