题目内容
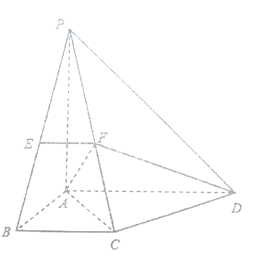
【题目】如图,在三棱柱![]() 中,底面
中,底面![]() 为正三角形,侧棱
为正三角形,侧棱![]() 底面
底面![]() .已知
.已知![]() 是
是![]() 的中点,
的中点, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析 (Ⅱ)见解析(Ⅲ)![]()
【解析】试题分析:(Ⅰ)由![]() ,
, ![]() 及
及![]() ,可证
,可证![]() 平面
平面![]() .即可证明
.即可证明
平面![]() 平面
平面![]() ;
;
(Ⅱ)证明![]() .又因为
.又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]()
(Ⅲ)由![]() 即可求得三棱锥
即可求得三棱锥![]() 的体积.
的体积.
试题解析:
(Ⅰ)证明:由已知![]() 为正三角形,且D是BC的中点,
为正三角形,且D是BC的中点,
所以![]() .
.
因为侧棱![]() 底面
底面![]() ,
, ![]() ,
,
所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
而![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)证明:连接![]() ,设
,设![]() ,连接
,连接![]() .
.
由已知得,四边形![]() 为正方形,则
为正方形,则![]() 为
为![]() 的中点.
的中点.
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]()
(Ⅲ)由(Ⅱ)可知![]() ∥平面
∥平面![]() ,
,
所以![]() 与
与![]() 到平面
到平面![]() 的距离相等,
的距离相等,
所以![]() .
.
由题设及![]() ,得
,得![]() ,且
,且![]() .
.
所以![]() ,
,
所以三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料溶化完毕时钢水的含碳量x与冶炼时间y(从炉料溶化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程.
(3)预报当钢水含碳量为160个0.01%时,应冶炼多少分钟?
参考公式:r=![]()
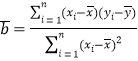 ,
,
线性回归方程![]()