题目内容
【题目】设数列![]() 满足
满足![]() ,其中
,其中![]() ,且
,且![]() ,
, ![]() 为常数.
为常数.
(1)若![]() 是等差数列,且公差
是等差数列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且存在
,且存在![]() ,使得
,使得![]() 对任意的
对任意的![]() 都成立,求
都成立,求![]() 的最小值;
的最小值;
(3)若![]() ,且数列
,且数列![]() 不是常数列,如果存在正整数
不是常数列,如果存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立. 求所有满足条件的数列
均成立. 求所有满足条件的数列![]() 中
中![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() (3)3
(3)3
【解析】试题分析:(1)利用等差数列定义将条件转化为公差关系,解方程可得![]() 的值;(2)先求
的值;(2)先求![]() 的值;即得数列为等比数列,分离变量将不等式恒成立问题转化为对应函数最值问题:
的值;即得数列为等比数列,分离变量将不等式恒成立问题转化为对应函数最值问题: ![]() ,即
,即![]() ,
, ![]() 最大值,再根据数列单调性确定
最大值,再根据数列单调性确定![]() 最大值,即得
最大值,即得![]() 的最小值;(3)本题由于求周期最小值,可以从小逐个验证即可:
的最小值;(3)本题由于求周期最小值,可以从小逐个验证即可: ![]() 为常数列,舍去;
为常数列,舍去; ![]() 时,可推得
时,可推得![]() ,舍去;
,舍去; ![]() 时,可取一个数列满足条件.
时,可取一个数列满足条件.
试题解析:解:(1)由题意,可得![]() ,
,
化简得![]() ,又
,又![]() ,所以
,所以![]() .
.
(2)将![]() 代入条件,可得
代入条件,可得![]() ,解得
,解得![]() ,
,
所以![]() ,所以数列
,所以数列![]() 是首项为1,公比
是首项为1,公比![]() 的等比数列,所以
的等比数列,所以![]() .
.
欲存在![]() ,使得
,使得![]() ,即
,即![]() 对任意
对任意![]() 都成立,
都成立,
则![]() ,所以
,所以![]() 对任意
对任意![]() 都成立.
都成立.
令![]() ,则
,则![]() ,
,
所以当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 的最大值为
的最大值为![]() ,所以
,所以![]() 的最小值为
的最小值为![]() .
.
(3)因为数列![]() 不是常数列,所以
不是常数列,所以![]() .
.
①若![]() ,则
,则![]() 恒成立,从而
恒成立,从而![]() ,
, ![]() ,所以
,所以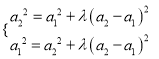 ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,可得
,可得![]() 是常数列.矛盾.
是常数列.矛盾.
所以![]() 不合题意.
不合题意.
②若![]() ,取
,取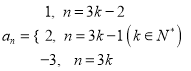 (*),满足
(*),满足![]() 恒成立.
恒成立.
由![]() ,得
,得![]() .
.
则条件式变为![]() .
.
由![]() ,知
,知![]() ;
;
由![]() ,知
,知![]() ;
;
由![]() ,知
,知![]() .
.
所以,数列(*)适合题意.
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目



