题目内容
8．5本不同的数，全部分给四个学生，每个学生至少1本，不同分法的种数为240．分析 由题意知先把5本书中的两本捆起来看做一个元素，这一个元素和其他的三个元素在四个位置全排列，根据分步计数原理两个过程的结果数相乘得到结果．
解答 解：由题意知先把5本书中的两本捆起来看做一个元素共有C52，
这一个元素和其他的三个元素在四个位置全排列共有A44，
∴分法种数为C52•A44=240．
故答案为：240．
点评 本题考查排列组合问题在几何中的应用，在计算时要求做到，兼顾所有的条件，先排约束条件多的元素，做的不重不漏，注意实际问题本身的限制条件．
练习册系列答案
相关题目
18．设F1，F2为椭圆$\frac{x^2}{4}+{y^2}$=1的两个焦点，点P在椭圆上，若线段PF1的中点在y轴上，则$\frac{{|{P{F_2}}|}}{{|{P{F_1}}|}}$的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{7}$ | D． | $\frac{1}{9}$ |
16．设集合M={x|2x2-y2=1}，N={y|y=x2}，则M∩N=（ ）
| A． | {（1，1）} | B． | {（-1，1），（1，1）} | C． | $[{\frac{1}{2}，+∞}）$ | D． | $[{\frac{{\sqrt{2}}}{2}，+∞}）$ |
13．若（2x-1）2015=a0+a1x+a2x2+…+a2015x2015（x∈R），则$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2015}}}}{{{2^{2015}}{a_1}}}$的值为（ ）
| A． | $\frac{1}{2015}$ | B． | -$\frac{1}{2015}$ | C． | $\frac{1}{4030}$ | D． | -$\frac{1}{4030}$ |
20．知a1=1，an+1=$\frac{a_n}{{3{a_n}+1}}$，则数列{an}的通项为an=（ ）
| A． | $\frac{1}{2n-1}$ | B． | 2n-1 | C． | $\frac{1}{3n-2}$ | D． | 3n-2 |
17．
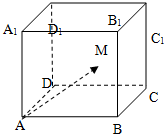如图，在棱长为2的正方体ABCD-A1B1C1D1内（含正方体表面）任取一点M，则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1内（含正方体表面）任取一点M，则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是（ ）| A． | $\frac{5}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |