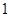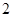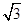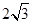题目内容
双曲线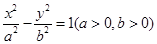 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为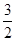 ,其中A
,其中A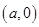 ,B
,B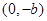 .
.
(1)求双曲线的方程;
(2)若B1是双曲线虚轴在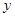 轴正半轴上的端点,过B1作直线与双曲线交于
轴正半轴上的端点,过B1作直线与双曲线交于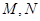 两点,求
两点,求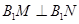 时,直线
时,直线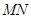 的方程.
的方程.
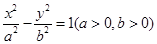 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为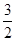 ,其中A
,其中A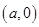 ,B
,B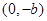 .
.(1)求双曲线的方程;
(2)若B1是双曲线虚轴在
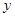 轴正半轴上的端点,过B1作直线与双曲线交于
轴正半轴上的端点,过B1作直线与双曲线交于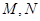 两点,求
两点,求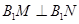 时,直线
时,直线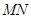 的方程.
的方程.(1)所求双曲线方程: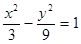

(2)所求的直线方程式为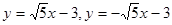
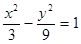

(2)所求的直线方程式为
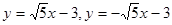
本题考查双曲线方程和直线方程的求法,解题时要认真审题,注意直线与双曲线位置关系的灵活运用,合理地进行等价转化。
(1)由A(a,0),B(0,-b),设直线AB,由此能求出双曲线方程.
(2)由双曲线方程为:
设P(x0,y0),则k1k2 =3.由B(0,-3)B1(0,3),设M(x1,y1),N(x2,y2),设直线l:y=kx-3,则 y=kx-3与3x2-y2=9,由此入手能求出直线MN的方程。
(1)由A(a,0),B(0,-b),设直线AB,由此能求出双曲线方程.
(2)由双曲线方程为:
设P(x0,y0),则k1k2 =3.由B(0,-3)B1(0,3),设M(x1,y1),N(x2,y2),设直线l:y=kx-3,则 y=kx-3与3x2-y2=9,由此入手能求出直线MN的方程。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
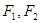 是双曲线
是双曲线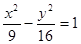 的两个焦点,点
的两个焦点,点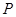 在双曲线上,且
在双曲线上,且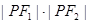
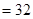 ,求证:
,求证:
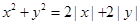 围成的图形的面积为_______________。翰林汇
围成的图形的面积为_______________。翰林汇 在坐标轴上,离心率为
在坐标轴上,离心率为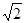 ,且过点(4,-
,且过点(4,-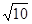 )(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证:
)(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证: .(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
.(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分) 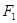 、
、 ,以
,以 为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )
为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )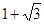
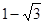

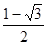
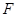 是抛物线
是抛物线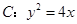 的焦点,过
的焦点,过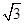 的直线交
的直线交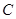 于
于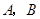 两点.设
两点.设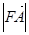 <
<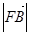 ,若
,若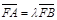 ,则λ的值为 .
,则λ的值为 . 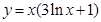 在点(1,1)处的切线方程为______
在点(1,1)处的切线方程为______ 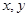 为正实数,
为正实数,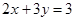 ,则
,则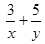 的最小值为 .
的最小值为 .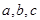 是直角三角形的三边(
是直角三角形的三边(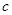 为斜边),则圆
为斜边),则圆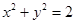 截直线
截直线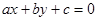 所得的弦长等于
所得的弦长等于