题目内容
已知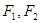 是双曲线
是双曲线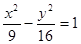 的两个焦点,点
的两个焦点,点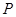 在双曲线上,且
在双曲线上,且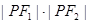
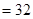 ,求证:
,求证:
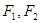 是双曲线
是双曲线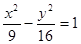 的两个焦点,点
的两个焦点,点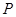 在双曲线上,且
在双曲线上,且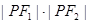
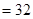 ,求证:
,求证:
见解析
试题分析:因为
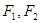 是双曲线
是双曲线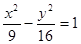 的两个焦点,点
的两个焦点,点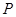 在双曲线上,
在双曲线上,所以有
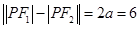 .
.平方得:
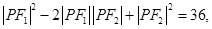
又因为
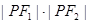
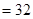 ,所以
,所以
而
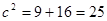 ,那么
,那么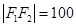 ,即
,即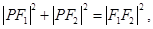
故
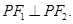
点评:双曲线上的点满足
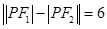 ,这一性质经常用到,可以帮助解题,应该准确灵活应用.
,这一性质经常用到,可以帮助解题,应该准确灵活应用.
练习册系列答案
相关题目
题目内容
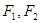 是双曲线
是双曲线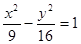 的两个焦点,点
的两个焦点,点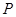 在双曲线上,且
在双曲线上,且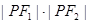
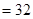 ,求证:
,求证:
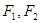 是双曲线
是双曲线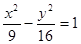 的两个焦点,点
的两个焦点,点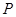 在双曲线上,
在双曲线上,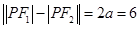 .
.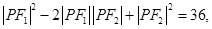
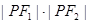
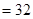 ,所以
,所以
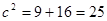 ,那么
,那么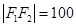 ,即
,即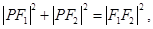
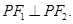
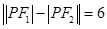 ,这一性质经常用到,可以帮助解题,应该准确灵活应用.
,这一性质经常用到,可以帮助解题,应该准确灵活应用.