题目内容
【题目】椭圆![]() (a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(1)求椭圆的方程;
(2)直线l:y=kx+m与椭圆交于点A,C,线段AC的中点为M,射线MO与椭圆交于点P,点O为△PAC的重心,求证:△PAC的面积S为定值;
【答案】(1)![]() 1;(2)见解析
1;(2)见解析
【解析】
(1)由题意得b=c,BF1=2,求出a、b后即可得解;
(2)设A(x1,y1),B(x2,y2),P(x0,y0),联立方程组得![]() ,
,![]() ,由题意x0
,由题意x0![]() ,y0
,y0![]() ,△PAC的面积
,△PAC的面积![]()
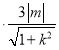 ,化简即可得证.
,化简即可得证.
(1)根据题意,由△BF1F2为等腰直角三角形可得b=c,
直线BF1:y=x+b被圆x2+y2=b2所截得的弦长为2,即BF1=2,
所以a=2,![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() 1;
1;
(2)证明:直线l的方程为y=kx+m,设A(x1,y1),B(x2,y2),
联立![]() ,可得(1+2k2)x2+4kmx+2m2﹣4=0,
,可得(1+2k2)x2+4kmx+2m2﹣4=0,
x1+x2![]() ,x1x2
,x1x2![]() ,y1+y2=k(x1+x2)+2m
,y1+y2=k(x1+x2)+2m![]() ,
,
由题意点O为△PAC重心,设P(x0,y0),可得![]() 0,
0,![]() 0,
0,
所以x0=-(x1+x2)![]() ,y0=-(y1+y2)
,y0=-(y1+y2)![]() ,
,
代入椭圆![]() 1;得
1;得![]() 1,化为2m2=1+2k2,
1,化为2m2=1+2k2,
设坐标原点O到直线l的距离为d,
则△PAC的面积S![]() |AC|3d
|AC|3d![]() |x1﹣x2|
|x1﹣x2|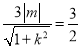 |m||x1﹣x2|
|m||x1﹣x2|![]() |m|
|m|
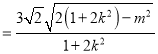 |m|=3
|m|=3![]()
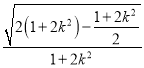
![]() .
.
可得△PAC的面积S为定值![]() .
.

【题目】2018年双11当天,某购物平台的销售业绩高达2135亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为X.
①求随机变量X的分布列;
②求X的数学期望和方差.
附:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |