Question

【题目】如图所示，该几何体是由一个直三棱柱ABE﹣DCF和一个四棱锥P﹣ABCD组合而成，其中EF＝EA＝EB＝2，AE⊥EB，PA＝PD，平面PAD∥平面EBCF．

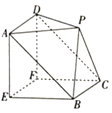
（1）证明：平面PBC∥平面AEFD；

（2）求直线AP与平面PCD所成角的正弦值．

Answer 1

【答案】（1）见解析（2）．

【解析】

（1）取EF中点O，BC中点G，AD中点H，连结OH，PH，OG，PG，证明OH∥PG，AD∥BC，故得证.

（2）以O为原点，OE为x轴，OG为y轴，OH为z轴，建立空间直角坐标系，计算平面PCD的法向量，借助线面角的向量公式即得解.

证明：取EF中点O，BC中点G，AD中点H，连结OH，PH，OG，PG，

由题意得PH2＝OH＝OG，

∴PHOG，∴四边形PHOG是平行四边形，∴OH∥PG，

∵ABDC，∴四边形ABCD是平行四边形，∴AD∥BC，

∵AD∩OH＝H，BC∩PG＝G，

∴平面PBC∥平面AEFD．

以O为原点，OE为x轴，OG为y轴，OH为z轴，建立空间直角坐标系，

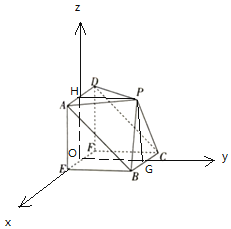
则A（1，0，2），P（0，2，2），C（﹣1，2，0），D（﹣1，0，2），

（1，﹣2，0），（﹣1，0，﹣2），（﹣1，﹣2，0），

设平面PCD的法向量（x，y，z），

则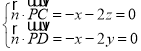，取x＝2，得（2，﹣1，﹣1），

设直线AP与平面PCD所成角为θ，

则sinθ．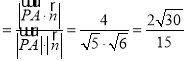

∴直线AP与平面PCD所成角的正弦值为．