题目内容
【题目】已知函数![]() (
(![]() 为常数),方程
为常数),方程![]() 有两个实根3和4,
有两个实根3和4,
(1)求![]() 的解析式;
的解析式;
(2)设![]() ,解关于x的不等式
,解关于x的不等式![]() ;
;
(3)已知函数![]() 是偶函数,且
是偶函数,且![]() 在
在![]() 上单调递增,若不等式
上单调递增,若不等式![]() 在任意
在任意![]() 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
【答案】(1)![]() (2)答案不唯一,见解析;(3)
(2)答案不唯一,见解析;(3)![]()
【解析】
(1)根据题意,方程f(x)﹣x+12=0即(1﹣a)x2+(12a﹣b)x+12b=0的两根为3和4,由根与系数的关系分析可得有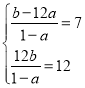 ,解可得a、b的值,即可得到答案;
,解可得a、b的值,即可得到答案;
(2)根据题意,原不等式变形可得f(x)![]() ,分情况讨论k的取值范围,求出不等式的解集,综合即可得答案;
,分情况讨论k的取值范围,求出不等式的解集,综合即可得答案;
(3)根据题意,由函数奇偶性与单调性的性质可得g(mx+1)≤g(x﹣2)|mx+1|≤|x﹣2|,x∈[![]() ,1];进而变形可得
,1];进而变形可得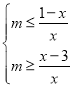 对于任给x∈[
对于任给x∈[![]() ,1]上恒成立,据此分析可得答案.
,1]上恒成立,据此分析可得答案.
(1)由![]() 即
即![]() ,
,
即(1﹣a)x2+(12a﹣b)x+12b=0两根为3和4,
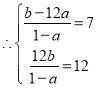 ,即
,即![]() .
.
![]()
故![]()
(2)由![]() 即
即![]()
1°当![]() 时,解集
时,解集![]()
2°当![]() 时,解集
时,解集![]()
3°当![]() 时,解集
时,解集![]()
(3)由于g(x)为偶函数且在(0,+∞)上递增,
g(mx+1)≤g(x﹣2)|mx+1|≤|x﹣2|,x∈[![]() ,1];
,1];
则有![]() ,变形可得
,变形可得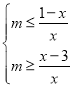 ,
,
即有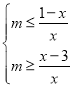 ,对于任给x∈[
,对于任给x∈[![]() ,1]上恒成立,
,1]上恒成立,
对于y![]() ,有
,有![]() =y|x=1=0,则有m≤0,
=y|x=1=0,则有m≤0,
对于y![]() ,有
,有![]() =y|x=1=﹣2,则有m≥﹣2,
=y|x=1=﹣2,则有m≥﹣2,
故﹣2≤m≤0,即m的取值范围为[﹣2,0].

练习册系列答案
相关题目

