题目内容
【题目】己知函数,![]() .
.
(1)画出![]() 的大致图象,并根据图象写出函数
的大致图象,并根据图象写出函数![]() 的单调区间;
的单调区间;
(2)当![]() 且
且![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)是否存在实数a,b,![]() 使得函数
使得函数![]() 在
在![]() 上的值域也是
上的值域也是![]() ?若存在,求出a,b的值,若不存在,说明理由.
?若存在,求出a,b的值,若不存在,说明理由.
【答案】(1)
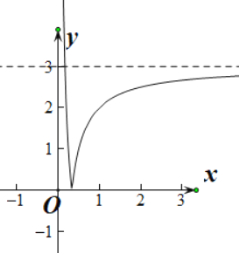
单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]()
(2) ![]() ;(3) 存在
;(3) 存在![]() 使得函数
使得函数![]() 在
在![]() 上的值域也是
上的值域也是![]()
【解析】
(1)根据函数图像的变换分析即可.
(2)根据(1)中图像可知,![]() 时
时![]() ,再根据对应的解析式求得
,再根据对应的解析式求得![]() 再代入
再代入![]() 求取值范围即可.
求取值范围即可.
(3)分![]() ,
,![]() 与
与![]() 三种情况分析即可.
三种情况分析即可.
(1) ![]() 可看做
可看做![]() 向下平移3个单位得到
向下平移3个单位得到
![]() .再将
.再将![]() 轴下方的图像沿
轴下方的图像沿![]() 轴向上翻折即可.
轴向上翻折即可.
注意零点为![]() 且以
且以![]() 为渐近线.
为渐近线.
故![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增
上单调递增
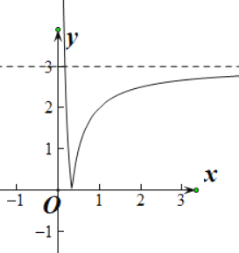
(2)由(1)中图像知,当![]() 时
时![]() ,且
,且![]() .
.
故![]() ,即
,即![]() .
.
令![]() ,因为
,因为![]() 故
故![]()
故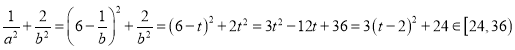 .
.
即![]() 的取值范围为
的取值范围为![]() .
.
(3)当![]() 时
时![]() ,故若存在实数a,b,使得函数
,故若存在实数a,b,使得函数![]() 在
在![]() 上的值域也是
上的值域也是![]() ,则
,则![]() 均不为
均不为![]() .
.
①当![]() 时,
时,![]() 为减函数,此时有
为减函数,此时有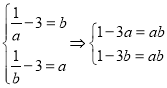 故
故![]() ,
,
不满足![]()
②当![]() 时,因为
时,因为![]() ,即
,即![]() 不满足.
不满足.
③当![]() 时, 此时
时, 此时![]() 故
故 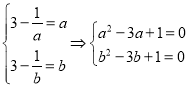 .
.
即![]() 是方程
是方程![]() 的两根.解得
的两根.解得![]() .满足
.满足![]() .
.
综上, 存在![]() 使得函数
使得函数![]() 在
在![]() 上的值域也是
上的值域也是![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目