题目内容
【题目】(1)已知一元二次方程![]() 的两根分别为2和
的两根分别为2和![]() ,求关于
,求关于![]() 的不等式
的不等式![]() 的解集.
的解集.
(2)求关于![]() 的不等式
的不等式![]() 的解集
的解集
【答案】(1) ![]() (2)答案不唯一,见解析
(2)答案不唯一,见解析
【解析】
(1)根据韦达定理![]() ,求
,求![]() ,代入不等式
,代入不等式![]() ,解分式不等式;
,解分式不等式;
(2)原不等式可化为![]() ,
,![]() 时,解不等式;当
时,解不等式;当![]() 时,方程
时,方程![]() 的两根为
的两根为![]() ,讨论两根的大小关系,解不等式.
,讨论两根的大小关系,解不等式.
解:(1)由韦达定理知,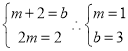
![]() 不等式为
不等式为![]() ,移项整理得
,移项整理得![]()
![]() ,解得
,解得![]()
![]() 不等式的解集为
不等式的解集为![]()
(2)由题意得,原不等式可化为![]()
(1)当![]() 时,原不等式的解集为
时,原不等式的解集为![]()
(2)当![]() 时,方程
时,方程![]() 的两根为
的两根为![]()
①当![]() 时,即
时,即![]() 时,原不等式的解集为
时,原不等式的解集为![]()
②当![]() 时,即
时,即![]() 时,原不等式的解集为
时,原不等式的解集为![]()
③当![]() 时,即
时,即![]() 时,原不等式的解集为
时,原不等式的解集为![]()
综上所述,当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;当0
;当0![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;当
;当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;当
;当![]() 时,原不等式的解集为
时,原不等式的解集为![]()

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
【题目】某车站在春运期间为了了解旅客购票情况,随机调查了100名旅客从开始在售票窗口排队到购到车票所用的时间![]() (以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图.
(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图.
频率 | 分组 | 频数 |
| 10 | 0.10 |
| 10 | ② |
| ① | 0.50 |
| 30 | 0.30 |
合计 | 100 | 1.00 |
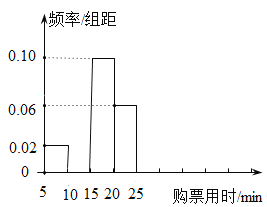
解答下列问题:
(1)在表中填写出缺失的数据并补全频率分布直方图;
(2)估计旅客购票用时的平均数.