题目内容
已知 所在的平面互相垂直,且AB=BC=BD,
所在的平面互相垂直,且AB=BC=BD, ,求:
,求:
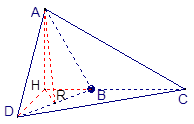
⑴.直线AD与平面BCD所成角的大小;
⑵.直线AD与直线BC所成角的大小;
⑶.二面角A-BD-C的余弦值.
 所在的平面互相垂直,且AB=BC=BD,
所在的平面互相垂直,且AB=BC=BD, ,求:
,求:
⑴.直线AD与平面BCD所成角的大小;
⑵.直线AD与直线BC所成角的大小;
⑶.二面角A-BD-C的余弦值.
⑴∠ADH=45°⑵90°⑶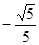
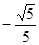
(1)本小题关键是找出线面角,在平面ABC内,过A作AH⊥BC,垂足为H,
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角.
(2)易证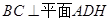 ,所以
,所以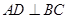 ,所以直线AD与直线BC所成角为
,所以直线AD与直线BC所成角为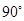 .
.
(3)找(做)出二面角A-BD-C的平面角是解决本小题的关键.本小题可采用三垂线定理定角法.过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角.
解:⑴如图,在平面ABC内,过A作AH⊥BC,垂足为H,
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角
由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,∴∠ADH=45°…………….5分
⑵∵BC⊥DH,且DH为AD在平面BCD上的射影, ∴BC⊥AD,
故AD与BC所成的角为90° ……9分
⑶过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角 设BC=a,则由题设知,AH=DH=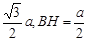 ,在△HDB中,HR=
,在△HDB中,HR=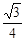 a,∴tanARH=
a,∴tanARH=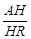 =2
=2
故二面角A—BD—C的余弦值的大小为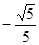 …………14分
…………14分
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角.
(2)易证
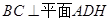 ,所以
,所以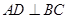 ,所以直线AD与直线BC所成角为
,所以直线AD与直线BC所成角为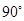 .
.(3)找(做)出二面角A-BD-C的平面角是解决本小题的关键.本小题可采用三垂线定理定角法.过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角.
解:⑴如图,在平面ABC内,过A作AH⊥BC,垂足为H,
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角
由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,∴∠ADH=45°…………….5分
⑵∵BC⊥DH,且DH为AD在平面BCD上的射影, ∴BC⊥AD,
故AD与BC所成的角为90° ……9分
⑶过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角 设BC=a,则由题设知,AH=DH=
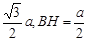 ,在△HDB中,HR=
,在△HDB中,HR=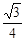 a,∴tanARH=
a,∴tanARH=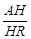 =2
=2故二面角A—BD—C的余弦值的大小为
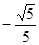 …………14分
…………14分
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
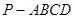 的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.
的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.
 与平面
与平面 ,在平面
,在平面 ,使
,使 中,侧棱
中,侧棱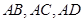 两两垂直,
两两垂直, 的
的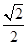 、
、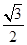 、
、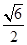 .则三棱锥
.则三棱锥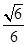
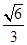
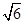
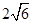
 作与直线
作与直线 成
成 角的直线共有( )条
角的直线共有( )条 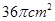 ,则这个球的体积为
,则这个球的体积为 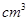 。
。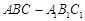 中,
中,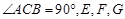 分别是
分别是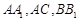 的中点,且
的中点,且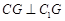 .
. 平面
平面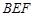 ;
;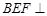 平面
平面 .
.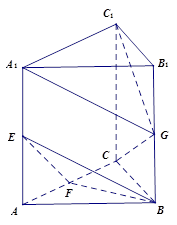
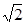 BC,E、F分别为CD、PB的中点。
BC,E、F分别为CD、PB的中点。