题目内容
在三棱锥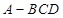 中,侧棱
中,侧棱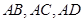 两两垂直,
两两垂直,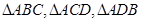 的
的
面积分别为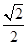 、
、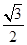 、
、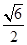 .则三棱锥
.则三棱锥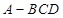 的体积为( )
的体积为( )
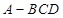 中,侧棱
中,侧棱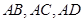 两两垂直,
两两垂直,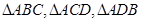 的
的面积分别为
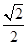 、
、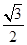 、
、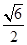 .则三棱锥
.则三棱锥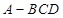 的体积为( )
的体积为( )A.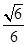 | B.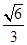 | C.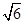 | D.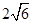 |
A
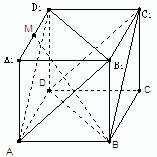
因为将三棱锥转化到长方体中,设长宽高的值分别为x,y,z,那么利用三角形的面积可知x,,y,z,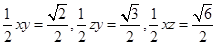 然后利用长方体的体积公式解得为
然后利用长方体的体积公式解得为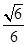 ,选A
,选A
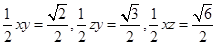 然后利用长方体的体积公式解得为
然后利用长方体的体积公式解得为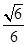 ,选A
,选A
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
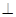 AD且AB=AD=
AD且AB=AD=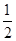 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
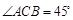 ,
,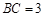 ,过动点A作
,过动点A作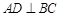 ,垂足
,垂足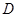 在线段
在线段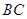 上且异于点
上且异于点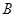 ,连接
,连接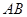 ,沿
,沿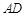 将△
将△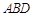 折起,使
折起,使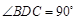 (如图2所示).
(如图2所示). 
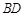 的长为多少时,三棱锥
的长为多少时,三棱锥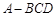 的体积最大;
的体积最大;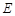 ,
,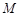 分别为棱
分别为棱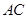 的中点,试在棱
的中点,试在棱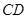 上确定一点
上确定一点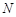 ,使得
,使得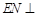
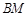 ,并求
,并求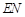 与平面
与平面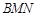 所成角的大小.
所成角的大小.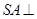 平面ABC,
平面ABC, 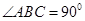 ,
, 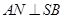 于N,
于N, 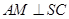 于M.
于M.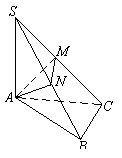
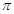 cm2
cm2  所在的平面互相垂直,且AB=BC=BD,
所在的平面互相垂直,且AB=BC=BD,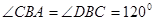 ,求:
,求: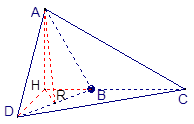
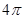 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积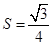 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为