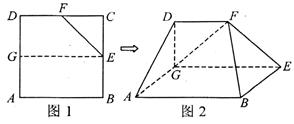
题目内容
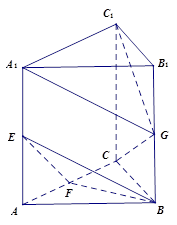
如图,在直三棱柱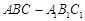 中,
中,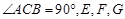 分别是
分别是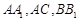 的中点,且
的中点,且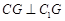 .
.
(1)求证: 平面
平面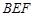 ;
;
(2)求证:平面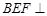 平面
平面 .
.
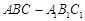 中,
中,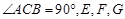 分别是
分别是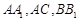 的中点,且
的中点,且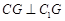 .
.(1)求证:
 平面
平面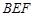 ;
;(2)求证:平面
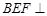 平面
平面 .
.
(1)略 (2)略
本试题主要是考查了线面平行的判定和面面垂直的判定的综合运用。
(1)利用线面平行的判定定理,只要得到线线平行即可。
(2)对于面面垂直的判定,自然要通过线面垂直来判定面面垂直,或者建立空间直角坐标系,利用法向量与法向量的垂直来判定。
解:(1)连结AG, 交BE于点M, 连结FM ……………2分
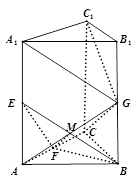
∵E, G分别为棱的中点
∴四边形ABGE为平行四边形,
∴点M为BE的中点, ……………4分
而点F为AC的中点,∴FM∥CG
∵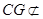 面BEF,
面BEF, 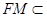 面BEF, ∴
面BEF, ∴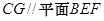 ;………7分
;………7分
(2因为三棱柱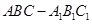 是直三棱柱,,
是直三棱柱,,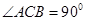
∴A1C1⊥面BC1,而CG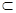 面BC1∴A1C1⊥CG, ………….………10分
面BC1∴A1C1⊥CG, ………….………10分
又∵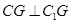 ,∴CG⊥面A1C1G由(1)知,FM∥CG∴FM⊥面A1C1G, ………12分
,∴CG⊥面A1C1G由(1)知,FM∥CG∴FM⊥面A1C1G, ………12分
而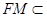 面BEF, ∴平面
面BEF, ∴平面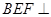 平面
平面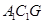
(1)利用线面平行的判定定理,只要得到线线平行即可。
(2)对于面面垂直的判定,自然要通过线面垂直来判定面面垂直,或者建立空间直角坐标系,利用法向量与法向量的垂直来判定。
解:(1)连结AG, 交BE于点M, 连结FM ……………2分

∵E, G分别为棱的中点
∴四边形ABGE为平行四边形,
∴点M为BE的中点, ……………4分
而点F为AC的中点,∴FM∥CG
∵
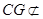 面BEF,
面BEF, 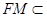 面BEF, ∴
面BEF, ∴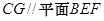 ;………7分
;………7分(2因为三棱柱
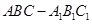 是直三棱柱,,
是直三棱柱,,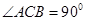
∴A1C1⊥面BC1,而CG
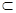 面BC1∴A1C1⊥CG, ………….………10分
面BC1∴A1C1⊥CG, ………….………10分又∵
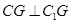 ,∴CG⊥面A1C1G由(1)知,FM∥CG∴FM⊥面A1C1G, ………12分
,∴CG⊥面A1C1G由(1)知,FM∥CG∴FM⊥面A1C1G, ………12分而
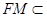 面BEF, ∴平面
面BEF, ∴平面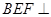 平面
平面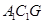

练习册系列答案
相关题目
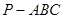 中,
中,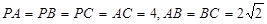
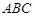 ⊥平面
⊥平面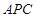
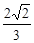 ,求BM的最小值.
,求BM的最小值.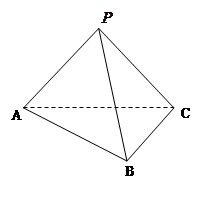
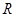 的球体完全装入底面半径是
的球体完全装入底面半径是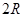 的圆柱形桶中,则桶的最小高度是 .
的圆柱形桶中,则桶的最小高度是 . 所在的平面互相垂直,且AB=BC=BD,
所在的平面互相垂直,且AB=BC=BD,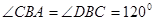 ,求:
,求: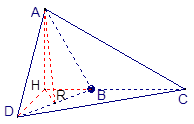
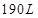 ,假如它的两底面边长分别等于
,假如它的两底面边长分别等于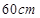 和
和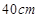 ,求它的深度为多少
,求它的深度为多少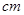 ?
?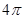 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积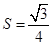 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为  中,
中, ,且
,且 分别是
分别是 的中点。
的中点。
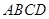 绕点
绕点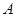 逆时针旋转
逆时针旋转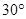 到正方形
到正方形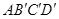 ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )