题目内容
10.已知x∈[$\frac{π}{2}$,π],且sin(2x-$\frac{π}{2}$)=$\frac{1}{3}$,则cos2x=-$\frac{1}{3}$,sinx=$\frac{\sqrt{6}}{3}$,tanx=-$\sqrt{2}$.分析 已知等式利用诱导公式化简求出cos2x的值,根据二倍角的余弦函数公式求出sinx的值,进而求出cosx的值,再利用同角三角函数间的基本关系求出tanx的值即可.
解答 解:∵x∈[$\frac{π}{2}$,π],sin(2x-$\frac{π}{2}$)=-cos2x=$\frac{1}{3}$,
∴2x-$\frac{π}{2}$∈[$\frac{π}{2}$,$\frac{3π}{2}$],cos2x=-$\frac{1}{3}$,
∴cos2x=1-sin2x=$\frac{1}{3}$,即sin2x=$\frac{2}{3}$,
解得:sinx=$\frac{\sqrt{6}}{3}$,cosx=-$\sqrt{1-si{n}^{2}x}$=-$\frac{\sqrt{3}}{3}$,
则tanx=-$\sqrt{2}$.
故答案为:-$\frac{1}{3}$;$\frac{\sqrt{6}}{3}$;-$\sqrt{2}$
点评 此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
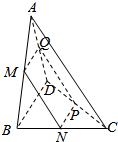 用平行于四面体ABCD的-组对棱AC和BD的平面截此四面体.得一四边形MNPQ.如图所示.
用平行于四面体ABCD的-组对棱AC和BD的平面截此四面体.得一四边形MNPQ.如图所示.