题目内容
20.在△ABC中,已知a=3,B=105°,C=15°,求此三角形最大边长的值.分析 由B与C的度数求出A的度数,利用正弦定理求出b的长,即为最大边长.
解答 解:∵在△ABC中,a=3,B=105°,C=15°,
∴A=60°,b为最大边,且sinB=sin(45°+60°)=$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
由正弦定理得:$\frac{a}{sinA}$=$\frac{b}{sinB}$,即$\frac{3}{\frac{\sqrt{3}}{2}}$=$\frac{b}{\frac{\sqrt{6}+\sqrt{2}}{4}}$,
则b=2$\sqrt{3}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$=$\frac{3\sqrt{2}+\sqrt{6}}{2}$.
点评 此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
11.下列图形均表示两个相交平面,其中画法正确的是( )
| A. | 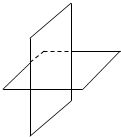 | B. | 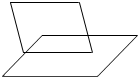 | C. | 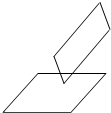 | D. |  |
 在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.
在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.