题目内容
1.已知f(x)=asinx+btanx+3满足f($\frac{π}{5}$)=5,求f($\frac{99π}{5}$)分析 由条件利用诱导公式求得 asin$\frac{π}{5}$+b•tan$\frac{π}{5}$=2,再根据诱导公式求得f($\frac{99π}{5}$)=-asin$\frac{π}{5}$-b•tan$\frac{π}{5}$+3,可得结果.
解答 解:∵f(x)=asinx+btanx+3满足f($\frac{π}{5}$)=asin$\frac{π}{5}$+b•tan$\frac{π}{5}$+3=5,∴asin$\frac{π}{5}$+b•tan$\frac{π}{5}$=2.
∴f($\frac{99π}{5}$)=asin$\frac{99π}{5}$+b•tan$\frac{99π}{5}$+3=asin(-$\frac{π}{5}$)+b•tan(-$\frac{π}{5}$)+3=-asin$\frac{π}{5}$-b•tan$\frac{π}{5}$+3=-2+3=1.
点评 本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若集合A={x|x=$\frac{k}{3}$,k∈Z},B={x|x=$\frac{k}{6}$,k∈Z},则( )
| A. | A$\underset{?}{≠}$B | B. | A$\underset{?}{≠}$B | C. | A=B | D. | A与B无公共元素 |
16.已知在锐角三角形ABC中,α+$\frac{π}{3}$的终边经过点P(sinB-cosA,cosB-sinA),且sin(α+$\frac{π}{3}$)=-$\frac{2\sqrt{2}}{3}$,则sin($\frac{2015π}{2}$+α)的值为( )
| A. | $\frac{2\sqrt{6}-1}{6}$ | B. | $\frac{1-2\sqrt{6}}{6}$ | C. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}-2\sqrt{2}}{6}$ |
6.在一个文艺比赛中,12名专业人士和12名观众代表各组成一个评判小组,给参赛选手打分.下面是两个评判组对同一名选手的打分:
(1)解释如何衡量每一组成员的相似性.
(2)对每一组计算这种相似性的度量值.你能据此判断小组A与小组B哪一个更像是由专业人士组成的吗?
| 小组A | 42 | 45 | 48 | 46 | 52 | 47 | 49 | 55 | 42 | 51 | 47 | 45 |
| 小组B | 55 | 36 | 70 | 66 | 75 | 49 | 46 | 68 | 42 | 62 | 58 | 47 |
(2)对每一组计算这种相似性的度量值.你能据此判断小组A与小组B哪一个更像是由专业人士组成的吗?
13.设不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ y≤-kx+4k\end{array}\right.$在平面直角坐标系中所表示的区域的面积为S,则当k>1时,$\frac{kS}{k-1}$的最小值为( )
| A. | 16 | B. | 32 | C. | 48 | D. | 56 |
11.下列图形均表示两个相交平面,其中画法正确的是( )
| A. | 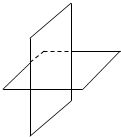 | B. | 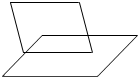 | C. | 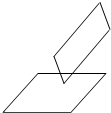 | D. |  |