题目内容
19.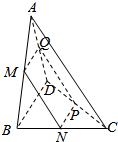 用平行于四面体ABCD的-组对棱AC和BD的平面截此四面体.得一四边形MNPQ.如图所示.
用平行于四面体ABCD的-组对棱AC和BD的平面截此四面体.得一四边形MNPQ.如图所示.(1)求证:四边形MNPQ是平行四边形;
(2)若AC=BD.能截得菱形吗?如何截?
(3)在什么情况下,可以截得-个矩形?
(4)在什么情况下,能截得-个正方形呢?如何截?
(5)若AC=BD=a,求证:?MNPQ的周长为定值.
分析 (1)根据线面平行的性质定理,便可得到AC∥MN,AC∥PQ,BD∥NP,BD∥MQ,这便得出四边形MNPQ为平行四边形;
(2)菱形便是四条边相等,从而看出M,N,P,Q分别为棱AB,BC,CD,DA的中点时,所得四边形为菱形;
(3)矩形就是平行四边形的一个内角为直角,这样可看出当AC⊥BD时截得的便是矩形;
(4)正方形要满足四条边相等,还得是矩形,从而满足(2)(3)即可;
(5)可设$\frac{AM}{AB}=b$,然后根据相似三角形的对应边的比例关系可求出平行四边形MNPQ的邻边长,从而求得周长,并可得出周长为定值.
解答 解:(1)∵BD∥平面MNPQ,BD?平面ABD,平面ABD∩平面MNPQ=MQ;
∴BD∥MQ;
同理,BD∥NP,AC∥MN,AC∥PQ;
∴MQ∥NP,MN∥PQ;
∴四边形MNPQ为平行四边形;
(2)能截得菱形,要截得菱形,则M,N,P,Q分别是棱AB,BC,CD,DA的中点;
(3)当AC⊥BD时,这两异面直线所成的角为90°,∴∠NMQ=90°,四边形MNPQ为矩形;
(4)当M,N,P,Q分别为棱AB,BC,CD,DA中点,且AC⊥BD时,截得的为正方形;
(5)证明:若$\frac{AM}{AB}=b$,则,MQ=ab,MN=(1-b)a;
∴?MNPQ的周长为2[(ab+(1-b)a]=2a;
∴即?MNPQ的周长为定值.
点评 考查线面平行的性质定理,三角形的对应边的比例关系,菱形的定义,以及矩形、正方形的定义.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
9.若集合A={x|x=$\frac{k}{3}$,k∈Z},B={x|x=$\frac{k}{6}$,k∈Z},则( )
| A. | A$\underset{?}{≠}$B | B. | A$\underset{?}{≠}$B | C. | A=B | D. | A与B无公共元素 |
7.“a=2”是“{1,a}⊆{1,2,3}”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.下列图形均表示两个相交平面,其中画法正确的是( )
| A. | 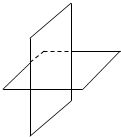 | B. | 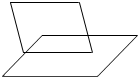 | C. | 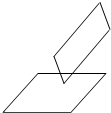 | D. |  |