题目内容
9.海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.| 地区 | A | B | C |
| 数量 | 50 | 150 | 100 |
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
(3)若在B,C两地区的5件样品中随机抽取3件进行进一步检测,求这3件商品恰有1件来自C地区的概率.
分析 (1)先计算出抽样比,进而可求出这6件样品来自A,B,C各地区商品的数量;
(2)先计算在这6件样品中随机抽取2件的基本事件总数,及这2件商品来自相同地区的事件个数,代入古典概型概率计算公式,可得答案;
(3)求出这3件商品恰有1件来自C地区的事件个数,代入古典概型概率计算公式,可得答案.
解答 解:(1)A,B,C三个地区商品的总数量为50+150+100=300,
故抽样比k=$\frac{6}{300}$=$\frac{1}{50}$,
故A地区抽取的商品的数量为:$\frac{1}{50}$,×50=1;
B地区抽取的商品的数量为:$\frac{1}{50}$,×150=3;
C地区抽取的商品的数量为:$\frac{1}{50}$,×100=2;
(2)在这6件样品中随机抽取2件共有:${C}_{6}^{2}$=15个不同的基本事件,且这些事件是等可能发生的,
记“这2件商品来自相同地区”为事件A,则这2件商品可能都来自B地区或C地区,
则A中包含${C}_{2}^{2}+{C}_{3}^{2}$=4种不同的基本事件,故P(A)=$\frac{4}{15}$,
即这2件商品来自相同地区的概率为$\frac{4}{15}$.
(3)这3件商品恰有1件来自C地区的概率为$\frac{{C}_{3}^{2}{C}_{2}^{1}}{{C}_{5}^{3}}$=$\frac{3}{5}$.
点评 本题考查的知识点是分层抽样,古典概型概率计算公式,难度不大,属于基础题.

练习册系列答案
相关题目
2.设向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(m,m+1),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{b}$•($\overrightarrow{a}$+$\overrightarrow{b}$)等于( )
| A. | 0 | B. | $\frac{5}{9}$ | C. | $\frac{29}{9}$ | D. | 5 |
17.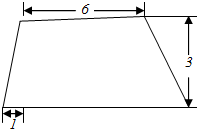 已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
 已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )| A. | 37 | B. | 74 | C. | 111 | D. | 222 |
18.一个几何体的三视图如图所示,则该几何体的体积为( )
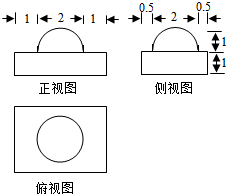

| A. | 12+$\frac{π}{3}$ | B. | 12+$\frac{2π}{3}$ | C. | 12+π | D. | 12+$\frac{4π}{3}$ |
19.定义在N*上的函数f(x)满足f(1)=1,且f(n+1)=$\left\{\begin{array}{l}{\frac{1}{2}f(n),n为偶数}\\{f(n),n为奇数}\end{array}\right.$,则f(22)=( )
| A. | $\frac{1}{1024}$ | B. | $\frac{1}{512}$ | C. | $\frac{1}{2048}$ | D. | 1 |
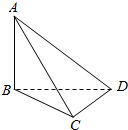 如图,三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为$\sqrt{2}$.
如图,三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为$\sqrt{2}$.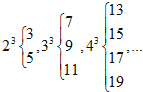 仿此,若m3的“分裂”数中有一个是73,则m的值为9.
仿此,若m3的“分裂”数中有一个是73,则m的值为9.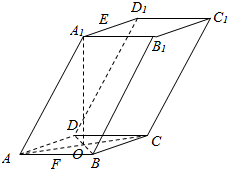 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AB=1,∠DAB=60°,AA1=$\sqrt{3}$,BD中点为O,A1O⊥平面ABCD,E、F分别为A1D1,AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AB=1,∠DAB=60°,AA1=$\sqrt{3}$,BD中点为O,A1O⊥平面ABCD,E、F分别为A1D1,AB的中点.