题目内容
4．
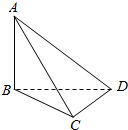如图，三棱锥A-BCD中，AB⊥平面BCD，BC⊥CD，若AB=BC=CD=2，则该三棱锥的侧视图（投影线平行于BD）的面积为$\sqrt{2}$．
分析 判断左视图的特征，利用几何体的数据求解面积即可．
解答 解：由三视图可知，左视图是直角三角形，直角边长为：2，$\sqrt{2}$；
左视图的面积为：$\frac{1}{2}×2×\sqrt{2}$=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查解得几何体的三视图，考查空间想象能力以及计算能力．
练习册系列答案
阅读快车系列答案
相关题目
16．在$\frac{1-cosα}{1+cosα}$=α中，α的取值范围是（ ）
| A． | α＜-1 | B． | α≥0 | C． | α＞-1 | D． | α＜0 |
12．已知函数f（x）=$\sqrt{3}$sin（2x+φ），若f（α）=$\sqrt{3}$，则（ ）
| A． | f（α+$\frac{5π}{6}$）＞f（α+$\frac{π}{12}$） | B． | f（α+$\frac{5π}{6}$）＜f（α+$\frac{π}{12}$） | C． | f（α+$\frac{5π}{6}$）=f（α+$\frac{π}{12}$） | D． | 大小与α，φ有关 |
9．海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．
（1）求这6件样品中来自A，B，C各地区商品的数量；
（2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．
（3）若在B，C两地区的5件样品中随机抽取3件进行进一步检测，求这3件商品恰有1件来自C地区的概率．
| 地区 | A | B | C |
| 数量 | 50 | 150 | 100 |
（2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．
（3）若在B，C两地区的5件样品中随机抽取3件进行进一步检测，求这3件商品恰有1件来自C地区的概率．
14．若曲线C1：x2+y2-2x=0与曲线C2：x（y-mx-m）=0有三个不同的公共点，则实数m的取值范围是（ ）
| A． | （0，$\sqrt{3}$） | B． | （-$\sqrt{3}$，0）∪（0，$\sqrt{3}$） | C． | （0，$\frac{{\sqrt{3}}}{3}$） | D． | （-$\frac{{\sqrt{3}}}{3}$，0）∪（0，$\frac{{\sqrt{3}}}{3}$） |