题目内容
【题目】(1)求与点P(3，5)关于直线l：x－3y＋2＝0对称的点P′的坐标．(2)已知直线l：y＝－2x＋6和点A(1，－1)，过点A作直线l1与直线l相交于B点，且|AB|＝5，求直线l1的方程．
【答案】(1) (5，－1) (2) x＝1或3x＋4y＋1＝0
【解析】(1)设P′(x0，y0)，则kPP′＝
，PP′中点为
.
∴
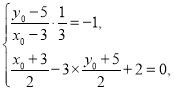解得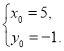
∴点P′坐标为(5，－1)．
(2)当直线l1的斜率不存在时，方程为x＝1，此时l1与l的交点B的坐标为(1，4)．|AB|＝
符合题意．
当直线l1的斜率存在时，设为k，则k≠－2，∴直线l1为y＋1＝k(x－1)，
则l1与l的交点B为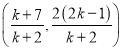
，
∴|AB|＝
，
解得k＝－
，∴直线l1为3x＋4y＋1＝0.
综上可得l1的方程为x＝1或3x＋4y＋1＝0.
练习册系列答案
名校课堂系列答案
相关题目
