题目内容
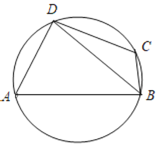
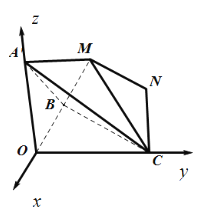
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
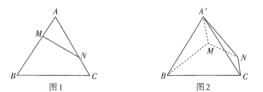
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
【答案】(1)见解析(2)见解析
【解析】
(1)要证明平面![]() 平面
平面![]() ,只需证明
,只需证明![]() 平面
平面![]() 即可;
即可;
(2)选择条件①②③之一,均需建系,算得向量![]() 以及平面
以及平面![]() 的法向量,设直线
的法向量,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,利用
,利用![]() 计算即可.
计算即可.
(1)由已知得![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
解得![]() ,故
,故![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,又∵
,又∵![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)(ⅰ)若用条件①![]() ,由(1)得
,由(1)得![]() ,
,![]() 和
和![]() 是两条相交直线,∴
是两条相交直线,∴![]() 平面
平面![]() .
.
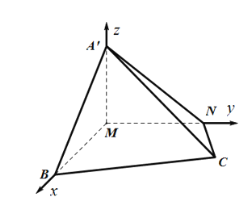
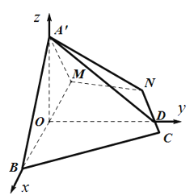
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,设
,设![]() ,其中
,其中![]() ,则
,则![]() .
.
平面![]() 的法向量为
的法向量为![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则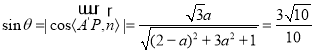 ,解得
,解得![]() ,
,
所以不存在![]() 满足条件.
满足条件.
(ⅱ)若用条件②二面角![]() 大小为
大小为![]() ,由(1)得
,由(1)得![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∴![]() .过
.过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() .
.
在平面![]() 中,作
中,作![]() ,点
,点![]() 在
在![]() 的右侧.
的右侧.
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则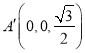 ,设
,设![]() ,其中
,其中![]() ,则
,则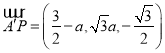 .
.
平面![]() 的法向量为
的法向量为![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则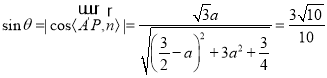 ,
,
解得![]() 或
或![]() (舍去),所以存在
(舍去),所以存在![]() 满足条件,这时
满足条件,这时![]() .
.
(ⅲ)若用条件③![]() ,在
,在![]() 中,由余弦定理得:
中,由余弦定理得:
![]() ,即
,即![]() ,
,
所以![]() ,故
,故![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() .
.
同(ⅱ)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则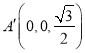 ,设
,设![]() ,其中
,其中![]() ,则
,则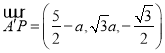 .
.
平面![]() 的法向量为
的法向量为![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则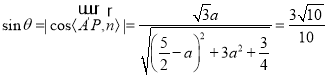 ,
,![]() .
.
解得![]() ,所以不存在
,所以不存在![]() 满足条件.
满足条件.
【点晴】
本题考查面面垂直的判定定理,以及利用向量法求线面角的问题,考查学生数学运算能力,空间想象能力,是一道中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】某生物研究所为研发一种新疫苗,在200只小白鼠身上进行科研对比实验,得到如下统计数据:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)能否有![]() 的把握认为注射此种疫苗有效?
的把握认为注射此种疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中,分别抽取3只进行病例分析,然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: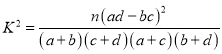 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】在党中央的正确领导下,通过全国人民的齐心协力,特别是全体一线医护人员的共同努力,新冠肺炎疫情得到了有效控制.作为集中医学观察隔离点的某酒店在疫情期间,为客人提供两种速食品—“方便面”和“自热米饭”.为调查这两种速食品的受欢迎程度,酒店部门经理记录了连续10天这两种速食品的销售量,得到如下频数分布表(其中销售量单位:盒):
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方便面 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 |
自热米饭 | 88 | 96 | 98 | 97 | 101 | 99 | 102 | 107 | 104 | 112 |
(1)根据两组数据完成下面的茎叶图(填到答题卡上);

(2)根据统计学知识,你认为哪种速食品更受欢迎,并简要说明理由;
(3)求自热米饭销售量y关于天数t的线性回归方程,并预估第12天自热米饭的销售量(结果精确到整数).
参考数据:![]() ,
,![]() .
.
附:回归直线方程![]() ,其中
,其中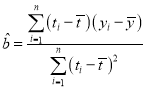 ,
,![]() .
.
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)