题目内容
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证: 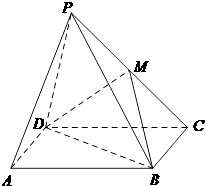
(1)PA∥平面MDB;
(2)PD⊥BC.
【答案】
(1)证明:连接AC,交BD与点O,连接OM,
∵M为PC的中点,O为AC的中点,
∴MO∥PA,
∵MO平面MDB,PA平面MDB,
∴PA∥平面MDB
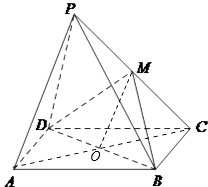
(2)证明:∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC平面ABCD,BC⊥CD,
∴BC⊥平面PCD,
∵PD平面PCD,
∴BC⊥PD
【解析】(1)连接AC,交BD与点O,连接OM,先证明出MO∥PA,进而根据线面平行的判定定理证明出PA∥平面MDB.(2)先证明出BC⊥平面PCD,进而根据线面垂直的性质证明出BC⊥PD.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目