Question

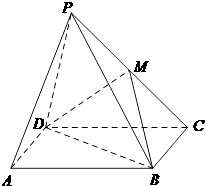
【题目】如图1所示，在Rt△ABC中，AC=6，BC=3，∠ABC=90°，CD为∠ACB的平分线，点E在线段AC上，CE=4．如图2所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连接AB，设点F是AB的中点．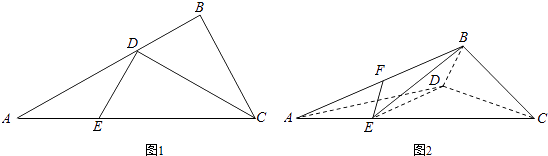
（1）求证：DE⊥平面BCD；
（2）若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥B﹣DEG的体积．

Answer 1

【答案】
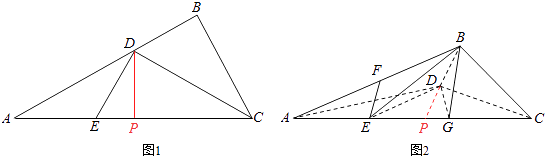
（1）解：取AC的中点P，连接DP，因为在Rt△ABC中，AC=6，BC=3，∠ABC=90°，CD为∠ACB的平分线，

所以∠A=30°，△ADC是等腰三角形，所以DP⊥AC，DP= ，∠DCP=30°，∠PDC=60°，

又点E在线段AC上，CE=4．所以AE=2，EP=1，所以∠EDP=30°，

∴∠EDC=90°，∴ED⊥DC；

∵将△BCD沿CD折起，使得平面BCD⊥平面ACD，平面BDC∩平面EDC=DC

∴DE⊥平面BCD

（2）解：若EF∥平面BDG，其中G为直线AC与平面BDG的交点，G为EC的中点，此时AE=EG=GC=2，

因为在Rt△ABC中，AC=6，BC=3，∠ABC=90°，CD为∠ACB的平分线，

所以BD= ，DC= ，

所以B到DC的距离h= = = ，

因为平面BCD⊥平面ACD，平面BDC∩平面EDC=DC，

所以B到DC的距离h就是三棱锥B﹣DEG的高．

三棱锥B﹣DEG的体积：V= = = =

【解析】（1）取AC的中点P，连接DP，证明DP⊥AC，∠EDC=90°，ED⊥DC；利用平面与平面垂直的性质证明DE⊥平面BCD；（2）说明G为EC的中点，求出B到DC的距离h，说明到DC的距离h就是三棱锥B﹣DEG的高．利用 ， 即可求三棱锥B﹣DEG的体积．
【考点精析】关于本题考查的直线与平面平行的判定和直线与平面垂直的判定，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案．