题目内容
已知数列{an}满足：an=logn+1（n+2）（n∈N*），定义使a1•a2•a3…ak为整数的数k（k∈N*）叫做企盼数，则区间[1，2013]内所有的企盼数的和为（ ）
| A．1001 | B．2026 | C．2030 | D．2048 |
∵an=logn+1（n+2）=
，（n∈N*），
∴a1•a2•a3…ak=
•
•
…
=log2（k+2），
又∵a1•a2•a3…ak为整数，
∴k+2必须是2的n次幂（n∈N*），即k=2n-2；
又k∈[1，2013]，∴1≤2n-2≤2013，∴取2≤n≤10；
∴区间[1，2013]内所有的企盼数的和为：
M=（22-2）+（23-2）+（24-2）+…+（210-2）=
-2×9=2026；
故选：B．
| log2(n+2) |
| log2(n+1) |
∴a1•a2•a3…ak=
| log23 |
| log22 |
| log24 |
| log23 |
| log25 |
| log24 |
| log2(k+2) |
| log2k |
又∵a1•a2•a3…ak为整数，
∴k+2必须是2的n次幂（n∈N*），即k=2n-2；
又k∈[1，2013]，∴1≤2n-2≤2013，∴取2≤n≤10；
∴区间[1，2013]内所有的企盼数的和为：
M=（22-2）+（23-2）+（24-2）+…+（210-2）=
| 22-211 |
| 1-2 |
故选：B．
练习册系列答案
相关题目
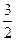n2+
n,则数列{an}的通项公式为________________.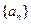
中，
，
．
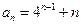项和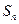
；（2）证明不等式
，对任意
+
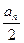(n∈N+),则其｛an｝的前10项和为