题目内容
已知数列{an}的前n项和为Sn=-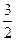 n2+
n2+ n,则数列{an}的通项公式为________________.
n,则数列{an}的通项公式为________________.
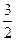 n2+
n2+ n,则数列{an}的通项公式为________________.
n,则数列{an}的通项公式为________________.-3n+104(n∈N*)
当n=1时,a1=S1=-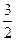 +
+ =101.
=101.
当n≥2时,an=Sn-Sn-1,
=(-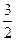 n2+
n2+ n)-[-
n)-[-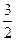 (n-1)2+
(n-1)2+ (n-1)]=-3n+104.
(n-1)]=-3n+104.
∵a1也满足an=-3n+104,
∴数列{an}的通项公式为an=-3n+104(n∈N*).
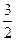 +
+ =101.
=101.当n≥2时,an=Sn-Sn-1,
=(-
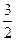 n2+
n2+ n)-[-
n)-[-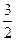 (n-1)2+
(n-1)2+ (n-1)]=-3n+104.
(n-1)]=-3n+104.∵a1也满足an=-3n+104,
∴数列{an}的通项公式为an=-3n+104(n∈N*).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
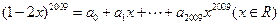 ,则
,则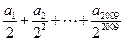 的值为( )
的值为( )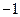
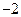
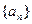
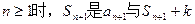
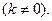
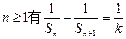 ;
;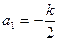 ,求Sn;
,求Sn;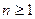 ,试证明:S1S2+S2S3+……+SnS
,试证明:S1S2+S2S3+……+SnS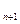
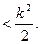
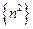 的前
的前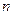 项和
项和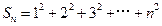 ,研究一下,能否找到求
,研究一下,能否找到求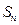 的一个公式.你能把你的思想方法作一些推广吗?
的一个公式.你能把你的思想方法作一些推广吗?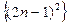 的前
的前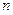 项和
项和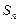 .
.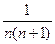 (n∈N*),若前n项的和为
(n∈N*),若前n项的和为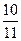 ,则项数n为 ____。
,则项数n为 ____。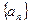 ,
,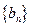 都是等差数列,其中
都是等差数列,其中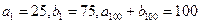 ,那么数列
,那么数列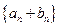 的前
的前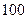 项的和是( ).
项的和是( ).


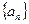 中,
中,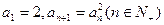 ,则数列
,则数列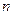 项和
项和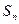 为 .
为 .