题目内容
设 .
.
(1)若 时,
时, 单调递增,求
单调递增,求 的取值范围;
的取值范围;
(2)讨论方程 的实数根的个数.
的实数根的个数.
 .
.(1)若
 时,
时, 单调递增,求
单调递增,求 的取值范围;
的取值范围;(2)讨论方程
 的实数根的个数.
的实数根的个数.(1)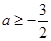 ;(2)见解析.
;(2)见解析.
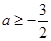 ;(2)见解析.
;(2)见解析.试题分析:(1)求出函数导数,当
 时,
时, 单调递增,说明当
单调递增,说明当 时,
时,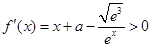 ,即
,即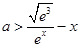 在
在 恒成立,又函数
恒成立,又函数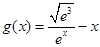 在
在 上递减,所以
上递减,所以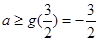 ;(2)将方程化为
;(2)将方程化为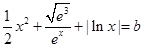 ,令
,令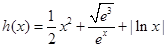 ,利用导数求出
,利用导数求出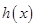 的单调区间,讨论
的单调区间,讨论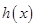 的取值当
的取值当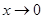 时,
时,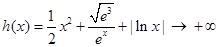 ,当
,当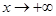 时,
时,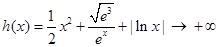 ,所以当
,所以当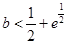 时,方程无解,当
时,方程无解,当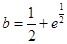 时,方程有一个根,当
时,方程有一个根,当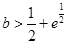 时,方程有两个根.
时,方程有两个根.试题解析:(1)∵
 ∴
∴ 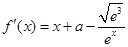
∵当
 时,
时, 单调递增 ∴当
单调递增 ∴当 时,
时,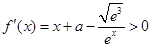
∴
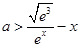 ,,函数
,,函数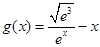 在
在 上递减
上递减∴
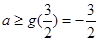
(2)
 ∴
∴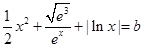
令
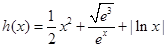
当
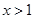 时
时 
∵
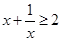
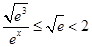 ∴
∴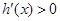
即
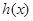 在
在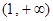 递增
递增当
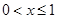 时
时 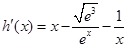
∵
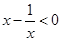
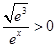 ∴
∴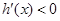
即
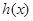 在
在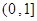 递减
递减∵
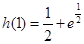
当
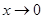 时
时 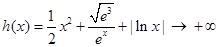
当
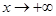 时
时 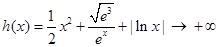
∴①当
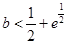 时,方程无解
时,方程无解②当
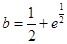 时,方程有一个根
时,方程有一个根③当
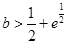 时,方程有两个根
时,方程有两个根
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
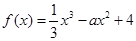 ,且
,且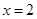 是函数
是函数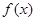 的一个极小值点.
的一个极小值点.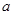 的值;
的值;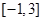 上的最大值和最小值.
上的最大值和最小值.
 ,其中
,其中 为实常数.
为实常数. 时,求函数
时,求函数 的单调区间;
的单调区间; 上的极值.
上的极值. 在
在 处有极小值,则实数
处有极小值,则实数 为 .
为 . 的最大值____________.
的最大值____________.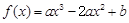 在区间
在区间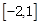 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求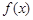 的解析式.
的解析式.