题目内容
【题目】若函数 ![]() .当x=2时,函数
.当x=2时,函数 ![]() 取得极值
取得极值 ![]() .
.
(1)求函数的解析式;
(2)若函数 ![]() =k有3个解,求实数k的取值范围.
=k有3个解,求实数k的取值范围.
【答案】
(1) ,所以 , .即12a-b=0,8a-2b+4= ,由此可解得 ,b=4 ∴
(2) , 所以 在x=-2处取得极大值 ,在x=2处取得极小值 所以
【解析】分析:求函数 ![]() 的定义域;(求函数
的定义域;(求函数 ![]() 的导数
的导数 ![]() ,令
,令 ![]() ,求方程
,求方程 ![]() 的所有实数根;考察
的所有实数根;考察 ![]() 在各实数根左、右的值的符号: ①如果在x0两侧
在各实数根左、右的值的符号: ①如果在x0两侧 ![]() 符号相同,则
符号相同,则 ![]() 不是
不是 ![]() 的极值点;②如果在
的极值点;②如果在 ![]() 附近的左侧
附近的左侧 ![]() ,右侧
,右侧 ![]() ,则
,则 ![]() 是极大值;③如果
是极大值;③如果 ![]() 在
在 ![]() 附近的左侧
附近的左侧 ![]() ,右侧
,右侧 ![]() ,那么
,那么 ![]() 是极小值.
是极小值.
【考点精析】解答此题的关键在于理解函数的极值的相关知识,掌握极值反映的是函数在某一点附近的大小情况.

练习册系列答案
相关题目
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
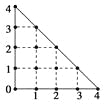
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.