题目内容
【题目】已知数列{an}的前n项和Sn=n2﹣n,数列{bn}的前n项和Tn=4﹣bn .
(1)求数列{an}和{bn}的通项公式;
(2)设cn= ![]() anbn , 求数列{cn}的前n项和Rn的表达式.
anbn , 求数列{cn}的前n项和Rn的表达式.
【答案】
(1)解:∵数列{an}的前n项和Sn=n2﹣n,
∴n=1时,a1=0;
n≥2时,an=Sn﹣Sn﹣1=n2﹣n﹣[(n﹣1)2﹣(n﹣1)]=2n﹣2,
n=1时也成立,
∴an=2n﹣2.
∵数列{bn}的前n项和Tn=4﹣bn,
∴n=1时,b1=4﹣b1,解得b1=2.
n≥2时,bn=Tn﹣Tn﹣1=4﹣bn﹣(4﹣bn﹣1),化为:bn= ![]() .
.
∴数列{bn}是等比数列,首项为2,公比为 ![]() .
.
∴bn= ![]() =
= ![]() .
.
(2)解:cn= ![]() anbn=
anbn= ![]() (2n﹣2)×
(2n﹣2)× ![]() =(n﹣1)×
=(n﹣1)× ![]() .
.
∴数列{cn}的前n项和Rn=0+1+2× ![]() +3×
+3× ![]() +…+(n﹣1)×
+…+(n﹣1)× ![]() .
.
![]() =
= ![]() +2×
+2× ![]() +…+(n﹣2)×
+…+(n﹣2)× ![]() +(n﹣1)×
+(n﹣1)× ![]() ,
,
∴ ![]() Rn=1+
Rn=1+ ![]() +…+
+…+ ![]() ﹣(n﹣1)×
﹣(n﹣1)× ![]() =
= 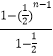 ﹣(n﹣1)×
﹣(n﹣1)× ![]() =2﹣(n+1)×
=2﹣(n+1)× ![]() .
.
∴Rn=4﹣(n+1)× ![]()
【解析】(1)利用递推关系可得an;利用递推关系与等比数列的通项公式可得bn . (2)利用“错位相减法”、等比数列的求和公式即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系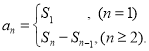 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目