题目内容
14.若函数f(x)=sin22x(x∈R)是( )| A. | 最小正周期为$\frac{π}{2}$的偶函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
分析 利用倍角公式化简函数解析式可得f(x)=-$\frac{1}{2}$cos4x+$\frac{1}{2}$,由周期公式可求最小正周期,由f(-x)=f(x)可得函数为偶函数,从而得解.
解答 解:∵f(x)=sin22x=$\frac{1-cos4x}{2}$=-$\frac{1}{2}$cos4x+$\frac{1}{2}$,
∴最小正周期T=$\frac{2π}{4}$=$\frac{π}{2}$,
∵由f(-x)=-$\frac{1}{2}$cos(-4x)+$\frac{1}{2}$=-$\frac{1}{2}$cos4x+$\frac{1}{2}$=f(x),可得函数为偶函数,
∴函数f(x)=sin22x(x∈R)是最小正周期为$\frac{π}{2}$的偶函数.
故选:A.
点评 本题主要考查了三角函数的周期性及其求法,考查了余弦函数的图象和性质,考查了倍角公式的应用,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.下列说法错误的是( )
| A. | 一个算法应包含有限的操作步骤,而不能是无限的 | |
| B. | 有的算法执行完后,可能有无数个结果 | |
| C. | 一个算法可以有0个或多个输入 | |
| D. | 算法中的每一步都是确定的,算法的含义是唯一的 |
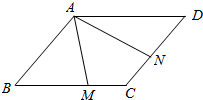 如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.
如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.