题目内容
3．若不等式kx2+2kx+2≥0对一切实数x恒成立，则实数k的取值范围为[0，2]．分析 对k进行分类讨论，当k=0时，显然成立，当k≠0时，则△=4k2-8k≤0，求解即可．
解答 解：∵kx2+2kx+2≥0对一切实数x恒成立，
当k=0时，显然成立，
当k≠0时，则
k＞0
△=4k2-8k≤0
∴0≤k≤2
故实数k的取值范围为[0，2]．
点评 考察了分类讨论和二次函数恒大于等于零问题，属于常规题型，应熟练掌握．
练习册系列答案
相关题目
14．若函数f（x）=sin22x（x∈R）是（ ）
| A． | 最小正周期为$\frac{π}{2}$的偶函数 | B． | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C． | 最小正周期为π的偶函数 | D． | 最小正周期为π的奇函数 |
11．设ξ是一个离散型随机变量，其分布列如下表：
则D（ξ）=$\frac{11}{16}$．
| ξ | -1 | 0 | 1 |
| P | 0.5 | 1-$\frac{3q}{2}$ | q2 |
8．下列命题中的说法正确的是（ ）
| A． | 命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1” | |
| B． | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C． | 命题“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1＞0” | |
| D． | 若命题p：?x0∈R，tanx0=1；命题q：?x∈R，x2-x+1＞0，则命题“p且q”是真命题 |
15．
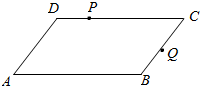如图在平行四边形ABCD中，已知AB=3，AD=2，∠DAB=60°，2$\overrightarrow{DP}$=$\overrightarrow{PC}$，$\overrightarrow{BQ}$=$\overrightarrow{QC}$，则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=（ ）
如图在平行四边形ABCD中，已知AB=3，AD=2，∠DAB=60°，2$\overrightarrow{DP}$=$\overrightarrow{PC}$，$\overrightarrow{BQ}$=$\overrightarrow{QC}$，则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=（ ）| A． | $\frac{13}{2}$ | B． | $\frac{15}{2}$ | C． | $\frac{17}{2}$ | D． | $\frac{19}{2}$ |