题目内容
5.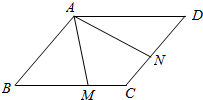 如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.
如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.(1)当λ=μ=$\frac{1}{2}$时,求|$\overrightarrow{a}$-$\overrightarrow{b}$|;
(2)若$\overrightarrow{a}$•$\overrightarrow{b}$=-2,求$\frac{1}{λ}$+$\frac{1}{μ}$的值.
分析 (1)$λ=μ=\frac{1}{2}$时,容易判断出M,N分别为BC,CD边的中点,从而得出$|\overrightarrow{a}-\overrightarrow{b}|=\frac{1}{2}|BD|$,根据四边形ABCD为菱形,及∠BAD=120°便可求出|BD|,从而得出|$\overrightarrow{a}-\overrightarrow{b}$|;
(2)根据λ,μ∈(0,1)便可知M,N分别在边BC,CD上,不包括端点,从而可求出$\overrightarrow{a}•\overrightarrow{b}=(\overrightarrow{AB}+λ\overrightarrow{BC})•(\overrightarrow{AD}+μ\overrightarrow{DC})$=-2,进行数量积的运算即可得出2λ+2μ=λμ,这样即可得出$\frac{1}{λ}+\frac{1}{μ}$的值.
解答 解:(1)$λ=μ=\frac{1}{2}$时,$\overrightarrow{BM}=\frac{1}{2}\overrightarrow{BC},\overrightarrow{DN}=\frac{1}{2}\overrightarrow{DC}$;
∴M,N分别是BC,CD的中点;
∴$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{AM}-\overrightarrow{AN}=\overrightarrow{NM}$;
∴$|\overrightarrow{a}-\overrightarrow{b}|=|\overrightarrow{NM}|=\frac{1}{2}|BD|$=$\sqrt{3}$;
(2)$\overrightarrow{a}=\overrightarrow{AM}=\overrightarrow{AB}+λ\overrightarrow{BC}$,$\overrightarrow{b}=\overrightarrow{AN}=\overrightarrow{AD}+μ\overrightarrow{DC}$;
∴$\overrightarrow{a}•\overrightarrow{b}=(\overrightarrow{AB}+λ\overrightarrow{BC})•(\overrightarrow{AD}+μ\overrightarrow{DC})$=$\overrightarrow{AB}•\overrightarrow{AD}+μ\overrightarrow{AB}•\overrightarrow{DC}+λ\overrightarrow{BC}•\overrightarrow{AD}$$+λμ\overrightarrow{BC}•\overrightarrow{DC}$=-2+4μ+4λ-2λμ=-2;
∴2μ+2λ=λμ;
∴$\frac{1}{λ}+\frac{1}{μ}=\frac{1}{2}$.
点评 考查向量加法、减法,及数乘的几何意义,向量长度的概念,三角形中位线的性质,以及数量积的运算及其计算公式.

| A. | 最小正周期为$\frac{π}{2}$的偶函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
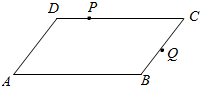 如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )| A. | $\frac{13}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{17}{2}$ | D. | $\frac{19}{2}$ |