题目内容
4.已知下列四个命题:①若函数y=f(x)在定义域上为减函数,则函数y=-f(x)在定义域上为增函数;
②若函数y=f(x)在定义域上为增函数,则函数g(x)=$\frac{1}{f(x)}$在其定义域内为减函数;
③若函数y=1+loga(x-1)图象过定点P(m,n),则logmn=0;
④若函数y=f(x)和y=g(x)在区间[-a,a]上都是奇函数,则函数y=f(x)•g(x)在区间[-a,a]上是偶函数,其中正确命题的序号是①④.
分析 ①由于函数y=f(x)与y=-f(x)的图象关于x轴对称即可得出;
②不一定正确,举反例如:f(x)=x;
③函数y=1+loga(x-1)图象过定点P(m,n),可得an-1=m-1.则logmn=0不一定成立,即可判断出正误;
④由于函数y=f(x)和y=g(x)在区间[-a,a]上都是奇函数,则函数f(-x)•g(-x)=-f(x)•[-g(x)]=f(x)g(x),即可判断出奇偶性.
解答 解:①若函数y=f(x)在定义域上为减函数,则函数y=-f(x)在定义域上为增函数,正确;
②若函数y=f(x)在定义域上为增函数,则函数g(x)=$\frac{1}{f(x)}$在其定义域内为减函数,不一定正确,例如f(x)=x;
③若函数y=1+loga(x-1)图象过定点P(m,n),则n=1+loga(m-1),化为an-1=m-1.则logmn=0不一定成立,因此不正确;
④若函数y=f(x)和y=g(x)在区间[-a,a]上都是奇函数,则函数f(-x)•g(-x)=-f(x)•[-g(x)]=f(x)g(x)在区间[-a,a]上是偶函数,正确.
其中正确命题的序号是①④.
故答案为:①④.
点评 本题考查了简易逻辑的判定方法、函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
14.若函数f(x)=sin22x(x∈R)是( )
| A. | 最小正周期为$\frac{π}{2}$的偶函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
15.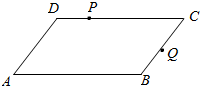 如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
 如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )| A. | $\frac{13}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{17}{2}$ | D. | $\frac{19}{2}$ |