题目内容
圆:x²+y²-4x+6y=0和圆:x²+y²-6x=0交于A,B两点,则AB的垂直平分线的方程是 ( )
| A.x+y+3=0 | B.2x-y-5="0" | C.3x-y-9=0 | D.4x-3y+7=0 |
C
试题分析:解:圆:x2+y2-4x+6y="0" 的圆心坐标为(2,-3),圆:x2+y2-6x=0的圆心坐标为(3,0),由题意可得AB的垂直平分线的方程就是两圆的圆心所在的直线的方程,由两点式求得AB的垂直平分线的方程是
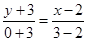 ,即3x-y-9=0,故答案为C
,即3x-y-9=0,故答案为C点评:本题主要考查用两点式求直线方程的方法,判断AB的垂直平分线的方程就是两圆的圆心所在的直线的方程,是解题的关键,属于基础题

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
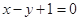 与圆
与圆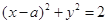 有公共点,则实数a取值范围是( )
有公共点,则实数a取值范围是( ) [1.+∞)
[1.+∞)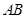 是
是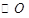 的直径,
的直径,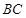 是
是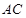 与
与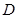 ,若
,若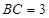 ,
,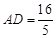 ,则
,则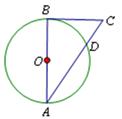
 是圆
是圆 的直径,
的直径, 是弦,
是弦, ,垂足为
,垂足为 ,
, 。
。
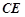 与圆
与圆 。
。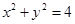 ,直线
,直线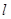 过点
过点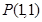 ,且与直线OP垂直,则直线
,且与直线OP垂直,则直线



 的最小值为 .
的最小值为 .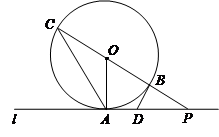
 (1)判断直线DB与⊙O的位置关系,并说明理由;
(1)判断直线DB与⊙O的位置关系,并说明理由;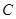 :
: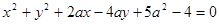 上所有的点均在第二象限内,则
上所有的点均在第二象限内,则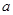 的取值范围为 。
的取值范围为 。 的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
. 
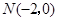 ,且与
,且与 的方程;
的方程; 斜率为
斜率为 的直线与曲线
的直线与曲线 两点,满足
两点,满足 ,求
,求