题目内容
已知直棱柱 中,底面
中,底面 为正方形,又
为正方形,又
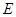 为
为 中点,则异面直线
中点,则异面直线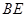 、
、 所成的角的余弦值为( )
所成的角的余弦值为( )
 中,底面
中,底面 为正方形,又
为正方形,又
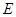 为
为 中点,则异面直线
中点,则异面直线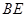 、
、 所成的角的余弦值为( )
所成的角的余弦值为( )A. | B. | C. | D. |
D
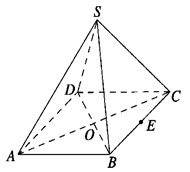
求异面直线所成的角,一般有两种方法,一种是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.还有一种方法是向量法,即建立空间直角坐标系,利用向量的代数法和几何法求解.本题采用几何法较为简单:连接A1B,则有A1B∥CD1,则∠A1BE就是异面直线BE与CD1所成角,由余弦定理可知cos∠A1BE的大小.

解:如图连接A1B,则有A1B∥CD1,
∠A1BE就是异面直线BE与CD1所成角,
设AB=1,
则A1E=AE=1,∴BE= ,A1B=
,A1B= .
.
由余弦定理可知:cos∠A1BE= =
= .
.
故选D.
本题主要考查了异面直线所成的角,考查空间想象能力和思维能力.

解:如图连接A1B,则有A1B∥CD1,
∠A1BE就是异面直线BE与CD1所成角,
设AB=1,
则A1E=AE=1,∴BE=
 ,A1B=
,A1B= .
.由余弦定理可知:cos∠A1BE=
 =
= .
.故选D.
本题主要考查了异面直线所成的角,考查空间想象能力和思维能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 。
。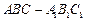
 中,已知
中,已知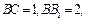
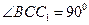 ,
,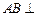 侧面
侧面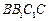 .
.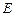 为棱
为棱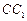 的中点,
的中点,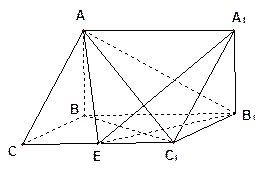
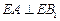 ;(2)若
;(2)若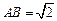 ,求二面角
,求二面角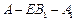 的大小.
的大小. 知平行四边形ABCD中,
知平行四边形ABCD中,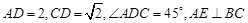 ,垂足为E,沿直线AE将△BAE翻折
,垂足为E,沿直线AE将△BAE翻折 成△B’AE,使得平面B’AE ⊥平面AECD.连接B’D,P是B’D上的点.
成△B’AE,使得平面B’AE ⊥平面AECD.连接B’D,P是B’D上的点.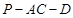 的余弦值
的余弦值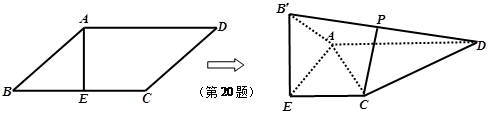
 是边长为1的正方体,求:
是边长为1的正方体,求:
 与平面
与平面 所成角的正切值;
所成角的正切值; 的大小;
的大小; 到平面
到平面 的距离。
的距离。 中,
中, 垂直于正方形
垂直于正方形 所在平面,
所在平面, 是
是 中点,
中点,
 平面
平面 ②求证:平面
②求证:平面 平面
平面 (13分)
(13分)
 的底面为直角梯形,
的底面为直角梯形, ,
, ,
, ,
, ,
, 平面
平面
 上是否存在一点
上是否存在一点 ,使平面
,使平面 平面
平面 ,如果存在,说明E点位置;如果不存在,说明理由.
,如果存在,说明E点位置;如果不存在,说明理由. 的余弦值.
的余弦值.