题目内容
(16分)如图,在底面是直角梯形的四棱锥P—ABCD中,AD∥BC,∠DAB=90º,PA⊥平面ABCD,PA=AB=BC=1,AD=2,M是PD的中点。
(1)求证:MC∥平面PAB;
(2)在棱PD上求一点Q,使二面角Q—AC—D的正切值为 。
。
(1)求证:MC∥平面PAB;
(2)在棱PD上求一点Q,使二面角Q—AC—D的正切值为
 。
。(1)过M作MN∥PA交AD于N,连接CN,
∵PA⊥平面ABCD且MP=MD,∴MN⊥平面ABCD且NA=ND,
∴AB=BC=AN=CN=1,
又∠NAB=90º,DA∥BC,∴四边形ABCN为正方形,
∴AB∥NC,∴平面PAB∥平面MNC。
∴MC∥平面PAB。
(2)在(1)中连接NB交AC于O,则NO⊥AC,连接MO,∵MN∥平面ABCD,
MO⊥AC,∴∠MON就是二面角M—AC—D的平面角,∵tan∠MON= ,
,
∴点M就是所求的Q点。
∵PA⊥平面ABCD且MP=MD,∴MN⊥平面ABCD且NA=ND,
∴AB=BC=AN=CN=1,
又∠NAB=90º,DA∥BC,∴四边形ABCN为正方形,
∴AB∥NC,∴平面PAB∥平面MNC。
∴MC∥平面PAB。
(2)在(1)中连接NB交AC于O,则NO⊥AC,连接MO,∵MN∥平面ABCD,
MO⊥AC,∴∠MON就是二面角M—AC—D的平面角,∵tan∠MON=
 ,
,∴点M就是所求的Q点。
略

练习册系列答案
相关题目
 、1
、1  、3
、3  、1或3
、1或3  、不确定
、不确定
 中,底面
中,底面 为正方形,又
为正方形,又
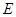 为
为 中点,则异面直线
中点,则异面直线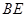 、
、 所成的角的余弦值为( )
所成的角的余弦值为( )



 ,则AD、BC所成的角等于
,则AD、BC所成的角等于 A、
A、 B、
B、 C、
C、  D、
D、
 柱
柱 中,
中, 侧棱与底面垂直,
侧棱与底面垂直, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.
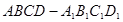 中,点
中,点 分别在线段
分别在线段 上,且
上,且  .以下结论:①
.以下结论:① ;②MN//平面
;②MN//平面 ;③MN与
;③MN与 异面;④点
异面;④点 到面
到面 的距离为
的距离为 ;⑤若点
;⑤若点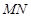 与
与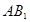 确定的平面在正方体
确定的平面在正方体
 的四个顶点都在半径为
的四个顶点都在半径为 的球面上,其中底面的三个顶点在该球的一个大圆上,球心为
的球面上,其中底面的三个顶点在该球的一个大圆上,球心为 ,
, 是线段
是线段 的中点,过
的中点,过