题目内容
已知点A(-1,0),B(0,2),点P是圆(x-1)2+y2=1上任意一点,则△PAB面积的最大值是( )
| A.2 | B.
| C.
| D.
|
根据题意画出图形,如图所示:
由直线AB的斜率kAB=
=2,
得到过P与AB平行且与圆相切的直线斜率k=2,
设该直线的方程为:y=2x+b,
又圆心坐标为(1,0),半径r=1,
所以圆心到直线的距离d=
=r=1,
即b=
-2(舍去)或b=-
-2,
故该直线方程为:y=2x-
-2,
又直线AB的方程为:y=2(x+1),即y=2x+2,
所以两平行线的距离为
,|AB|=
=
,
则△PAB面积的最大值是
×
×
=
.
故选B.

由直线AB的斜率kAB=
| 2-0 |
| 0-(-1) |
得到过P与AB平行且与圆相切的直线斜率k=2,
设该直线的方程为:y=2x+b,
又圆心坐标为(1,0),半径r=1,
所以圆心到直线的距离d=
| |b+2| | ||
|
即b=
| 5 |
| 5 |
故该直线方程为:y=2x-
| 5 |
又直线AB的方程为:y=2(x+1),即y=2x+2,
所以两平行线的距离为
| ||
|
| 12+22 |
| 5 |
则△PAB面积的最大值是
| 1 |
| 2 |
| 5 |
| ||
|
4+
| ||
| 2 |
故选B.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 相切,且在两坐标轴上截距相等的直线共有( )
相切,且在两坐标轴上截距相等的直线共有( ) 、
、 是方程
是方程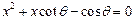 的两个不相等的实数根,那么过点
的两个不相等的实数根,那么过点 和点
和点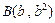 的直线与圆
的直线与圆 的位置关系是
的位置关系是  的左焦点为圆心,实轴长为半径的圆的标准方程为___________.
的左焦点为圆心,实轴长为半径的圆的标准方程为___________.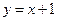 与圆
与圆 的位置关系为( )
的位置关系为( )