题目内容
已知直线l经过直线2x+y-5=0与x-2y=0的交点,
(1)点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值.
(1)点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值.
(1)经过两已知直线交点的直线系方程为
(2x+y-5)+λ(x-2y)=0,即(2+λ)x+(1-2λ)y-5=0,
∵点A(5,0)到l的距离为3,∴
=3.
即 2λ2-5λ+2=0,∴λ=2,或
,∴l方程为x=2或4x-3y-5=0.
(2)由
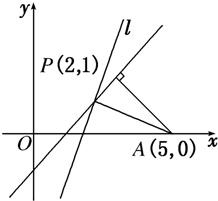
解得,交点P(2,1),如图,过P作任一直线l,设d为点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).
∴dmax=|PA|=
.
(2x+y-5)+λ(x-2y)=0,即(2+λ)x+(1-2λ)y-5=0,
∵点A(5,0)到l的距离为3,∴
| |10+5λ-5| | ||
|
即 2λ2-5λ+2=0,∴λ=2,或
| 1 |
| 2 |
(2)由
|
∴dmax=|PA|=
| 10 |


练习册系列答案
相关题目
 2=1
2=1 2+(y-1)2=1
2+(y-1)2=1 过点
过点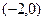 ,且与圆
,且与圆 相切,则
相切,则


