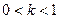题目内容
当x，θ∈R，M=（x+5-3|cosθ|）2+（x-2|sinθ|）2，则M能达到的最小值是（ ）
| A．5 | B．4
| C．2 | D．
|
因为要求M=（x+5-3|cosθ|）2+（x-2|sinθ|）2，则M能达到的最小值．
所以M是两点的距离的平方，转化为动点（-5+3|cosθ|，2|sinθ|）到直线y=x的距离的平方的最小值，
即
=
，显然当cosθ=1，sinθ=0时，
取得最小值为
．
所以M能达到的最小值是2．
故选C．
所以M是两点的距离的平方，转化为动点（-5+3|cosθ|，2|sinθ|）到直线y=x的距离的平方的最小值，
即
| M |
| |-5+3|cosθ|-2|sinθ|| | ||
|
| M |
| 2 |
所以M能达到的最小值是2．
故选C．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
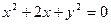的圆心C，且与直线x+y=0垂直的直线方程是（ ）
的最小值为________．
的取值范围
