题目内容
【题目】在数列{an}中,a1+2a2++22a3+…2n﹣1an=(n2n﹣2n+1)t对任意n∈N*成立,其中常数t>0.若关于n的不等式 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 的解集为{n|n≥4,n∈N*},则实数m的取值范围是 .
的解集为{n|n≥4,n∈N*},则实数m的取值范围是 .
【答案】[ ![]() )
)
【解析】解:当n≥2时,a1+2a2++22a3+…2n﹣1an=(n2n﹣2n+1)t…①
得a1+2a2++22a3+…2n﹣2an﹣1=[(n﹣1)2n﹣1﹣2n﹣1+1)t…②
将①,②两式相减,得 2n﹣1 an=(n2n﹣2n+1)t﹣[(n﹣1)2n﹣1﹣2n﹣1+1]t,
化简,得an=nt,其中n≥2.…(5分)
因为a1=t,所以an=nt,其中n∈N*.
∴ ![]() .
.
∴ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() =
= 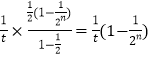
又∵ ![]() ,则关于n的不等式
,则关于n的不等式 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 化简为
化简为 ![]() .
.
当t>0时,考察不等式为 ![]() .的解,
.的解,
由题意,知不等式1﹣ ![]() >m的解集为{n|n≥4,n∈N*},
>m的解集为{n|n≥4,n∈N*},
因为函数y=1﹣ ![]() 在R上单调递增,所以只要求1﹣
在R上单调递增,所以只要求1﹣ ![]() 且1﹣
且1﹣ ![]() ≤m即可,∴
≤m即可,∴ ![]() .
.
所以,实数m的取值范围是[ ![]() ).
).
所以答案是:[ ![]() ).
).

练习册系列答案
相关题目