题目内容
【题目】圆上的点(2,1)关于直线x+y=0的对称点仍在圆上,且圆与直线x﹣y+1=0相交所得的弦长为 ![]() ,则圆的方程为 .
,则圆的方程为 .
【答案】(x﹣1)2+(y+1)2=5
【解析】解:设所求圆的圆心为(a,b),半径为r, ∵点A(2,1)关于直线x+y=0的对称点A′仍在这个圆上,
∴圆心(a,b)在直线x+y=0上,
∴a+b=0,①
且(2﹣a)2+(1﹣b)2=r2;②
又直线x﹣y+1=0截圆所得的弦长为 ![]() ,
,
且圆心(a,b)到直线x﹣y+1=0的距离为d= ![]() =
= ![]() ,
,
根据垂径定理得:r2﹣d2= ![]() ,
,
即r2﹣( ![]() )2=
)2= ![]() ③;
③;
由方程①②③组成方程组,解得 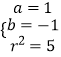 ;
;
∴所求圆的方程为(x﹣1)2+(y+1)2=5.
所以答案是:(x﹣1)2+(y+1)2=5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目